Mathematics Weblog
Zero
Sunday 29 February 2004 at 12:48 pm | In Articles | Post Comment- Why is
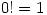 ?
? - By looking at
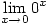 and at
and at 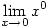 what can you say about
what can you say about 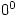 ?
? - Can
![\sqrt[0]{x} \sqrt[0]{x}](/maths/latexrender/pictures/952fb7f45b1f8cce3431cc164ac8a41d.gif) (the zeroth root of x) be defined? If so, how; if not, why?
(the zeroth root of x) be defined? If so, how; if not, why? - Criticise the following ‘proof’: If
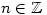 then
then 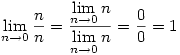
Powers and Logs
Monday 23 February 2004 at 8:10 pm | In Articles | Post CommentProve that 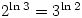
The proof should show you how this generalises. If you have studied group theory you can extend this even further by showing that 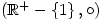 , where
, where  is defined by
is defined by 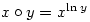 , is an abelian group.
, is an abelian group.
Why can’t 1 be an element of this group?
Factorials
Saturday 21 February 2004 at 11:06 pm | In Articles | Post CommentInspired by a test posting on S.O.S. Mathematics CyberBoard
Factorials are fascinating. They are obtained by multiplying the numbers 1, 2, 3, 4, 5 … together and are written using the ! sign. Thus
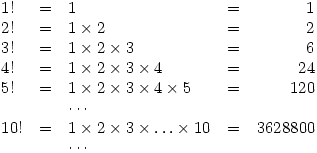
Factorials get large very quickly so 25! = 15 511 210 043 330 985 984 000 000 and as it gets larger there are more and more zeros.
Question: How can you find the number of zeros in 102! without calculating it?
Answer: All you do is count the number of times powers of 5 divide into 102 and add them up. So

Throw away the remainders and we get that there are 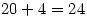 zeros in 102!
zeros in 102!
Now find how many zeros there are in 2004!
Can you show why this method works? Can you generalise it? Have a go, then look for answers on the internet.
Mathematicians will recognise this as a special case of
![\par\boxed{\begin{displaymath}
\textit{The highest power of a prime p dividing n! is }
\sum_{k=1}^\infty \left[\frac{n}{p^k}\right]
\hspace{0.5em}
\end{displaymath}} \par\boxed{\begin{displaymath}
\textit{The highest power of a prime p dividing n! is }
\sum_{k=1}^\infty \left[\frac{n}{p^k}\right]
\hspace{0.5em}
\end{displaymath}}](/maths/latexrender/pictures/a8aa8feb71aa03733c985da6c650a100.gif)
which is not difficult to prove by induction.
More on factorials at mathworld
Two Problems
Sunday 15 February 2004 at 3:34 pm | In Articles | Post CommentPress ‘read more’ below for the answers
1. Give an example of an easy calculation that most simple calculators get wrong
2. If 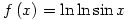 find
find 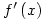 [Hint: think carefully about
[Hint: think carefully about 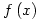 before you differentiate]
before you differentiate]
Millenium Problems
Sunday 8 February 2004 at 6:42 pm | In Articles | Post CommentMathematicians’ prime motive for research is not money which is just as well as there’s little money in it. However, there are 7 problems, the millenium problems for which there is a prize of $1 million for the solution to any of these problems. You can find out all about them at the Clay Mathematics Institute and in Keith Devlin’s book The Millennium Problems
Favourite Formula
Sunday 1 February 2004 at 6:18 pm | In Articles | 1 CommentWhy do mathematicians agree that 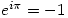 is their favourite formula? Read why at Euler’s Formula which is an excerpt from Keith Devlin’s excellent book Mathematics: the Science of Patterns then read the book!
is their favourite formula? Read why at Euler’s Formula which is an excerpt from Keith Devlin’s excellent book Mathematics: the Science of Patterns then read the book!
GIMPS
Sunday 1 February 2004 at 1:57 pm | In Articles | Post CommentThe Great International Mersenne Prime Search (GIMPS) wants you to help in their search for Mersenne primes. These are prime numbers of the form 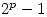 (where p is itself a prime) and they can be found by anyone! The largest
(where p is itself a prime) and they can be found by anyone! The largest 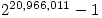 was found last November by a student. It has 6,320,430 decimal digits.
was found last November by a student. It has 6,320,430 decimal digits.
You could win fame and fortune so go along to http://www.mersenne.org/prime.htm where it says:
“You could discover one of the most coveted finds in all of Mathematics – a new Mersenne prime number. We’ve found six already. Join in on this fun, yet serious research project. All you need is a personal computer, patience, and a lot of luck.
In addition to the joy of making a mathematical discovery, you might win some cash. The Electronic Frontier Foundation is offering a $100,000 award to the first person or group to discover a ten million digit prime number! See how GIMPS will distribute this award if we are lucky enough to find a ten million digit prime.“
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^