Mathematics Weblog
Coin tossing is not fair
Saturday 20 March 2004 at 11:02 pm | In Articles | Post CommentIf you toss a coin and want it to come up heads then start with it heads up. 51% of the time it will come up heads. This remarkable result was discovered by a mathematician Persi Diaconis and you can hear an interview with him here (then click on All Things Considered audio link) where he talks about the lack of randomness of coin tossing.
It turns out that any randomness is just due to sloppy humans who toss coins differently every time. So all those text books on tossing coins are wrong and until now nobody had noticed!
See also Science News articles:
Division by zero shock!
Tuesday 16 March 2004 at 4:35 pm | In Articles | Post CommentIt is well known that division by zero is the ultimate mistake to make in mathematics (see Dividing by 0 and Wikipedia). Different rules may apply in other advanced number systems but for use in the set of real numbers it has to be avoided. Doing so is often not easy, but one has to live with the consequences.
It is thus a shock to see division by zero hidden in a question in the AQA A Level Mathematics Specimen P4 Paper. Question 7 starts with
- The function
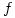 is defined by
is defined by 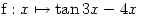 and has domain
and has domain 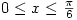
Where’s the division by zero? It is implicit in the definition of 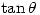 which is defined as
which is defined as 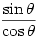 , provided of course that
, provided of course that 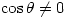 ; so what happens in the given domain? Thus
; so what happens in the given domain? Thus 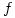 doesn’t exist, which makes the rest of the question unanswerable, since it requires you to differentiate and integrate
doesn’t exist, which makes the rest of the question unanswerable, since it requires you to differentiate and integrate 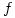 😀
😀
The examiners should have known better. Perhaps it is just as well that the syllabus (and hence the specimen paper) will be replaced, starting in 2004.
Thanks to one of my eagle-eyed students who spotted this horror!
Pi
Sunday 14 March 2004 at 6:35 pm | In Articles | Post CommentThe digits in the decimal of  have always intrigued mathematicans. In the computer age
have always intrigued mathematicans. In the computer age  has been calculated to billion of places. You can see the first 30 million digits at The Inverse Symbolic Calculator.
has been calculated to billion of places. You can see the first 30 million digits at The Inverse Symbolic Calculator.
 is known to be irrational (so the decimal expansion is infinite and non-recurring) and transcendental (so it is not a root of a polynomial equation with rational coefficients). You can see a proof on my page here. Yet it isn’t known if the digits are random in the statistical sense.
is known to be irrational (so the decimal expansion is infinite and non-recurring) and transcendental (so it is not a root of a polynomial equation with rational coefficients). You can see a proof on my page here. Yet it isn’t known if the digits are random in the statistical sense.
One of the things that doesn’t help in examining the decimal digits of  is that if you want to know, say, the 1000th decimal digit then you will have to calculate the previous 999.
is that if you want to know, say, the 1000th decimal digit then you will have to calculate the previous 999.
Note the word decimal in the last paragraph. If you go over to hex digits (base 16) then you can calculate any digit without knowing the previous ones. This truly remarkable result was discovered in 1996 by David Bailey, Peter Borwein and Simon Plouffe (their paper can be found here). What is astonishing is that the formula for  used to calcuate the nth is simple enough to be shown here:
used to calcuate the nth is simple enough to be shown here:
![\displaystyle \pi = \sum _{k=0} ^{\infty} \dfrac{1}{16^k} \left[\dfrac{4}{8k+1}-\dfrac{2}{8k+4}-\dfrac{1}{8k+5}-\dfrac{1}{8k+6}\right] \displaystyle \pi = \sum _{k=0} ^{\infty} \dfrac{1}{16^k} \left[\dfrac{4}{8k+1}-\dfrac{2}{8k+4}-\dfrac{1}{8k+5}-\dfrac{1}{8k+6}\right]](/maths/latexrender/pictures/a4391bf2245df0643d5600cfaa09cc4b.gif)
A program listing implementing this formula can be found here.
See Pi on the Web for lots more about  .
.
Whoops!
Monday 8 March 2004 at 1:34 pm | In Articles | Post CommentIn Advancing Maths For AQA: Pure Maths 2 (P2) there is the following question on page 121:
2. Find the gradient of the following curve at the point where 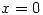
- (c)
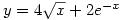
and gives an answer of 2 in the Answers section.
Spot the error.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^