Mathematics Weblog
Proof and logic
Sunday 24 October 2004 at 3:15 pm | In Articles | 3 CommentsMathematical proof is one of the topics that students find very difficult. Many of them assume what they are trying to prove, end up with a true statement and then think they have proved the result. Studying truth tables, particularly the implication operator may well help. See Logical Operations and Truth Tables
On a mathematics forum a student wanted to use its  facilities (provided by LatexRender of course 😎 ) to help a friend show how to prove
facilities (provided by LatexRender of course 😎 ) to help a friend show how to prove
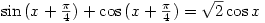
This is the original ‘proof’ they gave. Although they have now changed it I get the impression that I failed to convince them of the faulty logic; how would you explain what is wrong?
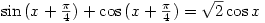
For this problem you need to know the addition formulas:
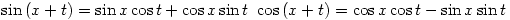
Using these formulas in the problem we can turn it into:
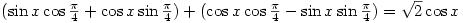
Then we use the fact that 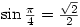 and
and 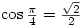
This changes it to:
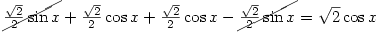
Here we cancelled out the terms that equals zero and then adding together what we have we end up with:
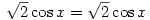
Some textbooks misuse infinity
Monday 18 October 2004 at 3:43 pm | In Articles | Post CommentIt’s happened again!  used in a textbook (unnamed to protect the guilty) as if it were a real number instead of an idea. In a discussion of the formula for the acute angle
used in a textbook (unnamed to protect the guilty) as if it were a real number instead of an idea. In a discussion of the formula for the acute angle 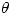 between two lines
between two lines
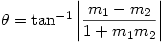
the following appears:
- Putting
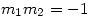 gives an angle
gives an angle 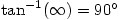 , confirming the condition for the lines to be perpendicular
, confirming the condition for the lines to be perpendicular This is of course complete nonsense. As I’ve said before 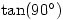 doesn’t exist and
doesn’t exist and 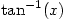 is only defined on
is only defined on 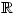 ie for
ie for 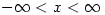
The textbook was written by the examiners (which is one reason why we use it); this worries me even more.
I suppose this is better than one well-known textbook back in the eighties which solved the equation 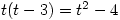 by putting
by putting 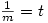 then ‘showing’
then ‘showing’  or
or 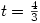 . This seems to show that all linear equations are quadratics in disguise; or cubics, quartics – who knows where this nonsense leads 😕
. This seems to show that all linear equations are quadratics in disguise; or cubics, quartics – who knows where this nonsense leads 😕
See also Division by zero shock!
Amazing Formula
Monday 11 October 2004 at 9:47 pm | In Articles | 3 CommentsThere are many interesting formulae in mathematics;
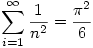
must be one of the most amazing of all.
The first reaction is where did that  come from? You can find 14 different proofs of this in a paper on Robin Chapman’s Home Page [look for Evaluating zeta(2)]
come from? You can find 14 different proofs of this in a paper on Robin Chapman’s Home Page [look for Evaluating zeta(2)]
Given this result can you prove another amazing result?
If you pick two positive integers at random, the probability of them having no common divisor is 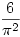
 gets everywhere! See Wikipedia for more such as
gets everywhere! See Wikipedia for more such as
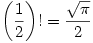 or
or 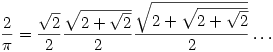 or
or 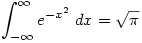
Primes
Sunday 10 October 2004 at 6:42 pm | In Articles | Post CommentEuclid’s proof that there are an infinite number of primes is a classic and as such appears as the first proof in Proofs from The Book.
Equally well-known is the formula (known as The Prime Number Theorem) which tells you that the number of primes 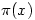 less than
less than 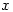 is given by
is given by 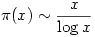 which means that the larger the value of
which means that the larger the value of 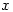 the closer (in a well-defined mathematical sense)
the closer (in a well-defined mathematical sense) 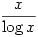 is to
is to 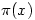 . This is quite hard to prove.
. This is quite hard to prove.
An easier, but non-trivial result, is Bertrand’s postulate which says that there is always a prime between  and
and 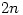 .
.
The fact that there are arbitrarily large gaps between successive primes is not difficult to prove. Suppose we want to find a gap between successive primes which is at least of size 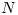 . Then we look at the numbers
. Then we look at the numbers

Then each of these numbers is not prime. Why? Look at 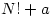 where
where 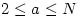 . Then
. Then 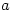 divides both
divides both 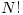 and
and 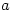 and so divides
and so divides 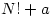 . Clearly
. Clearly 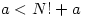 so
so 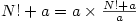 shows
shows 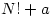 is not prime.
is not prime.
So we have a series of 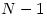 numbers all of which are not prime; thus the gap between a prime less than
numbers all of which are not prime; thus the gap between a prime less than 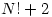 and a prime more than
and a prime more than 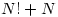 is at least
is at least 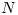 .
.
Error
Saturday 2 October 2004 at 10:04 pm | In Articles | 2 CommentsSix months ago in an article on the LambertW function I wrote:
- Thus
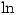 is defined by
is defined by 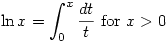 and it is then clear that, for example,
and it is then clear that, for example, 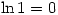
There’s a serious error in there which also completely invalidates it is then clear that …. Going back to the article the mistake leapt out at me – is it obvious to you? It’s strange how you read what you want to read rather than what is actually there 😕
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^