Mathematics Weblog
Martin Gardner’s Mathematical Games: The Entire Collection of His Scientific American Columns
Tuesday 28 December 2004 at 3:53 pm | In Articles | 10 CommentsMartin Gardner was an inspiration to many of us with his Scientific American articles. I remember devouring them avidly when I was at school many, many years ago. Some of the articles were published in various books, but now all of his columns are about to be published by The Mathematical Association of America on CD-ROM in February. American readers can pre-order it from Barnes & Noble and more details are available from Mathpuzzle.com.
Being able to read all his columns would be wonderful but I would still prefer to read it on old-fashioned paper. If it were published as a book in the UK, I would be the first to buy it.
In 1964, Scientific American devoted a complete issue to mathematics, so Martin Gardner devoted his column to word play
- … not discussed in any mathematical books, yet it has a about it a quasi-mathematical air … perhaps the combinatorial aspect is the reason why so many mathematicians are addicted to language play.
A few teasers he set from that issue:
- 1. The letters omitted from these common English words are all consonants
- _ _ _ E _ _ _ _ _
- _ A_ E _ I O U _ _ Y
2. I never did manage to find the missing letters (vowels or consonants) in
- _ _ M N O P _ _ _ _
3. He didn’t mention this word where the missing letters are again all consonants
- _ _ Y _ _ _ _
Billions of ’em
Friday 24 December 2004 at 12:10 am | In Articles | 5 CommentsI’ve long regretted the demise of the ‘British’ billion 1012, a million million, in favour of the US version which is 109, a thousand million. It means that the prefixes bi (billion), tri (trillion=million million million), quad (quadrillion) etc no longer make much sense. The change in the system is apparently due to the US adopting the French system (though France and French-speaking parts of North America changed again from 1948); international trade then did the rest. It’s all clearly explained at A Zillion Troubles (thanks to Gooseania for the link).
I sometimes ask my students to think about the size of numbers like a million and a billion (either version) by asking them to guess how long it would take to count to them at the rate of one per second without a break. Then they work it out on a calculator and 99% of their guesses are wildly out 😕
A Finite Discussion of Infinite Numbers
Wednesday 22 December 2004 at 11:03 pm | In Articles | 1 CommentKeith Devlin (British-born author of a number of interesting, well-written and highly recommended books) gives a 5-minute interview on NPR (a US radio station) about infinite numbers such as cardinal numbers like 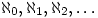 You can find the interview at A Finite Discussion of Infinite Numbers
You can find the interview at A Finite Discussion of Infinite Numbers
Simon Singh did a couple of series of short programmes about numbers on the BBC in March 2002 and October 2003. You can listen to his discussion of Infinity; there are links there to the other broadcasts as well as to other Science programmes. Worth listening to.
Some(6,7,8,9??) years ago there was a BBC radio series on the history of mathematics which was had me rolling about as it was so (intentionally) funny. Anyone remember it or know if it is available anywhere?
Student Howlers
Saturday 18 December 2004 at 8:06 pm | In Articles | 4 CommentsA couple of howlers seen in sci.math newsgroup some years ago
1. I do like the lateral (?) thinking behind this one 😀
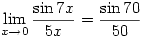
2. Problem
- Find
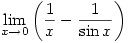
Answer
- Undefined
Proof:
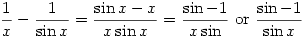
Therefore, since there are two possible answers with
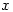 in the denominator and you can’t get rid of it and since
in the denominator and you can’t get rid of it and since 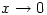 , the answer is undefined
, the answer is undefinedCancelling gives an example taken from Comic Sections by Desmond MacHale. Another one from the same book is:
3. Solve 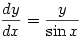
Solution:
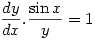 so
so 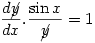 hence
hence 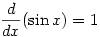 thus
thus 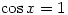 and
and 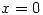
Do you have any favourite howlers?
2 unrelated problems
Sunday 12 December 2004 at 2:26 pm | In Articles | 2 Comments- Using the Gelfond-Schneider theorem show that if
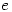 is transcendental then
is transcendental then  is transcendental
is transcendental - If
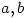 are positive integers such that
are positive integers such that 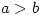 and
and 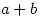 is even, show that
is even, show that 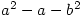 is not a square
is not a square
Notes
- This theorem was being discussed at a seminar many years ago as was the transcendence of
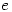 . When we were told that it was an obvious consequence that
. When we were told that it was an obvious consequence that  is transcendental we thought that the speaker was joking. When he showed how it followed, there was a moment’s silence and then applause – one of those moments when one realises that mathematics is such a wonderful subject.
is transcendental we thought that the speaker was joking. When he showed how it followed, there was a moment’s silence and then applause – one of those moments when one realises that mathematics is such a wonderful subject.
You can find an elementary proof (not using Gelfond-Schneider) of the transcendence of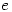 and
and  here
here
It’s interesting to note that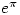 and
and 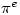 are very close. In fact
are very close. In fact 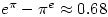 . See here
. See here - I came across this problem when looking through some old papers. I have no idea where it comes from (an old Mathematical Olympiad problem maybe??) or what the solution was.
Agnew’s Differential Equations
Sunday 5 December 2004 at 2:59 pm | In Articles | 3 CommentsWhen I studied differential equations, the set book was Ralph P Agnew’s Differential Equations. It had a brilliant index which seemed to contain every word in the book. Everything I ever wanted to look up was referenced in that index, unlike plenty of other textbooks.
It included a wonderful polemic about textbooks that claim that differential equations of order n have a general solution with n essential (aka arbitrary) constants:
- The promoted the view that to each differential equation of order n there corresponds an important family of solutions from which all other solutions … are obtainable by use of appropriate hocus-pocus involving envelopes and more complicated things. It was essential that this family of solutions should have a name (this is the start of the intimidation) which would immediately convince everybody that it existed and was important. With dubious regard for appropriateness of terminology, this family was called “the general solution” of the given equation.
He then says:
- It may be unclear whether this [differential equations of order n have n essential constants] is a theorem or a definition or merely a collection of words, but we are now in a realm where nearly everything is unclear. One thing, however, is clear. No meaning has been attached to the statement that a formula has n eseential constant. This gives the good old lecturer a chance to practice the art of proof by intimidation.
He then goes on to justify his remarks and includes as examples the differential equations 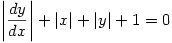 which has no solutions and
which has no solutions and 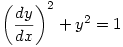 which has “vast hordes of real solutions“.
which has “vast hordes of real solutions“.
He also deals with the solution of 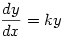 where dividing by
where dividing by 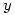 (the usual method taught at A level) won’t do since it could involve division by zero (the book indexes this as Division by zero taboo).
(the usual method taught at A level) won’t do since it could involve division by zero (the book indexes this as Division by zero taboo).
Finally, there is the wonderful snowplough problem (or snowplow as the author is American) which says:
- One day it started snowing at a heavy and steady rate. A snowplow started out at noon, going 2 miles the first hour and 1 mile the second hour. What time did it start snowing?
He says “Our first task is to recover from the shock of being asked to solve such a problem” and goes on “we assume that the plow clears snow at a constant rate of k cubic miles per hour“.
Now it’s up to you. Click on read more below for the time it started snowing.
Continue reading Agnew’s Differential Equations…
I really despair
Saturday 4 December 2004 at 8:50 pm | In Articles | 4 CommentsI came across this answer, written over a year ago, to a question about division by zero. The answer was written by a Physics instructor who seems to be rather confused.
- Division by zero is often defined as infinity. Infinity divided by zero is infinity-squared. For signs to be defined correctly, you must have a +0 and a -0. This is often accomplished through the theory of limits. The limit of x as x approaches zero from the negative side is -0. The limit of x as x approached zero from the positive side is +0. Higer (sic) level mathematics uses the concept of infinity quite often.
Let’s gloss over the first two appalling sentences. In the following sentences I suppose he is trying to refer to the fact that one can approach 0 (or any number) from different directions. If x approaches 0 from above, that is x remains positive, then you can write, for example, 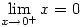 . Note that the limit is written as 0 not +0 which is of course equal to 0 so there’s no point writing it! This notation allows one to show that different things can happen if x approaches 0 from above or from below and to say that
. Note that the limit is written as 0 not +0 which is of course equal to 0 so there’s no point writing it! This notation allows one to show that different things can happen if x approaches 0 from above or from below and to say that 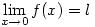 if and only if
if and only if 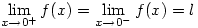 (where f is a real-valued function defined on a neighbourhood of 0).
(where f is a real-valued function defined on a neighbourhood of 0).
Personally, I like using 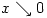 and
and  rather than
rather than 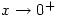 and
and 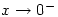 respectively, because they illustrate the approach from above or below.
respectively, because they illustrate the approach from above or below.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^