Mathematics Weblog
Divisors
Sunday 30 January 2005 at 8:25 pm | In Articles | 2 CommentsMost people, when asked how many divisors the number 60 has (including 1 and 60), would struggle to do so without listing them all. Yet once you know that the prime factorisation of 60 is 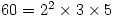 you can immediately say that the number of divisors is
you can immediately say that the number of divisors is 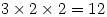 . In other words, you take each index, add 1 then multiply them together.
. In other words, you take each index, add 1 then multiply them together.
This is easy to see if you list the divisors as
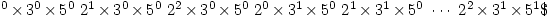
It’s then not difficult to prove the general result:
- If
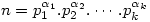 then the number of divisors of
then the number of divisors of  is
is 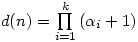
Quadratic Formula Song
Monday 24 January 2005 at 2:39 pm | In Articles | 1 CommentGot the blues about remembering 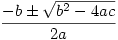 then listen to The Quadratic Formula Song at Calculus Music.
then listen to The Quadratic Formula Song at Calculus Music.
Tom Lehrer is the best known singing mathematician (zillions of pages on the net). Art Garfunkel (half of Simon & Garfunkel) will be known to older readers; he has an MA in mathematics and started a PhD but his music career came first.
A Million Random Digits With 100,000 Normal Deviates
Sunday 23 January 2005 at 11:52 am | In Articles | Post CommentMathematical humour is always welcome, particularly as it is rare. Who would have thought that a book of a million random numbers could inspire amusing reviews at Amazon.com?
Thanks to Isabel’s math blog.
Mathematical 404 Page
Sunday 16 January 2005 at 9:18 pm | In Articles | Post CommentGooseania spotted this mathematical 404 error page. Any others out there?
Four Colour Theorem Latest
Monday 10 January 2005 at 9:46 pm | In Articles | 2 CommentsListen to a short interview with Keith Devlin about the latest verification of the computer proof of the Four Colour Theorem at Solving the ‘Four-Color Problem’ of Map Making (near the bottom of the page). Then read more about it on Devlin’s Angle.
Thanks to Mathforge.net for alerting me to this.
Spherical Trigonometry
Saturday 8 January 2005 at 9:42 pm | In Articles | 8 CommentsThe idea that the angles of a triangle add up to 180° is so well engrained that it comes as a shock to some students that it isn’t true in other geometries. These geometries don’t have to be obscure or abstract since the angles of a spherical triangle drawn on the earth’s surface (assuming it is a sphere) always add up to more than 180° by an amount proportional to its area.
It’s a shame that like much else, spherical trigonometry has long since disappeared from the A level syllabus. The 2-dimensional sine rule
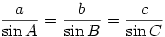
is (or ought to be 8-)) well-known but how many are aware of the 3-dimensional version
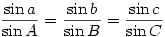
or the fact that the great circle distance (the shortest distance)  in nautical miles between points with latitude & longitude
in nautical miles between points with latitude & longitude 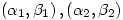 is given by
is given by
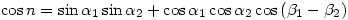
where  is measured in minutes? You could use sites such as Surface Distance Between Two Points of Latitude and Longitude but it’s not the same as sitting down and proving the general result.
is measured in minutes? You could use sites such as Surface Distance Between Two Points of Latitude and Longitude but it’s not the same as sitting down and proving the general result.
Without this introduction to three dimensions how is one going to start visualising geometry in four or more dimensions? Of course, reading Flatland would be an excellent start. Phoenix-Library has some excellent versions of this book in a number of online formats.
This is perhaps a suitable place to publicise my all time favourite puzzle:
- A hunter leaves his house one morning and walks one mile due south. He then walks one mile due west and shoots a bear, before walking a mile due north back to his house. What colour is the bear?
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^