Mathematics Weblog
4D Rubik’s Cube
Thursday 28 April 2005 at 11:05 pm | In Articles | Post CommentWho remembers Rubik’s cube? Rubik Unbound has an online version. Found that easy to solve? Then try the much harder 4-dimensional version at Magic Cube 4D Applet ❗
Magic Cube 4D says the normal version has 43 252 0032 274 489 856 000 unique positions whereas the 4D version has 1 756 772 880 709 135 843 168 526 079 081 025 059 614 484 630 149 557 651 477 156 021 733 236 798 970 168 550 600 274 887 650 082 354 207 129 600 000 000 000 000 unique positions, more than the number of atoms in the universe.
Similar Groups
Friday 22 April 2005 at 2:57 pm | In Articles | Post CommentStudents learning (finite) group theory often have to prove that 2 groups are isomorphic. They may construct a function from G to H, guided by their Cayley tables, then assume that the function is a homomorphism. Maybe they will check a few cases but don’t think it necessary to prove all 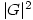 equations hold.
equations hold.
They are told that isomorphic groups have the same properties and, in particular, have the same number of elements of the same order. Unfortunately, they assume the converse is true which it isn’t. But the examples they see tend to confirm the converse; they don’t often see counter-examples.
To make things easier let’s say two finite groups G and H are similar if they have the same number of elements of the same order. I suspect this is entirely non-standard terminology 8-).
The counter-example of smallest order, 16, is where 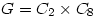 and
and 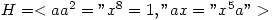 which are not isomorphic (G is abelian but H isn’t) but both groups have 1 element of order 1, 3 of order 2, 4 of order 4 and 8 of order 8.
which are not isomorphic (G is abelian but H isn’t) but both groups have 1 element of order 1, 3 of order 2, 4 of order 4 and 8 of order 8.
Other examples of non-isomorphic similar groups are:
- p is an odd prime:
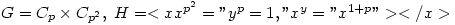 which have
which have 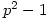 elements of order
elements of order 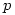 and
and 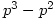 elements of order
elements of order 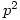
- p,q odd primes with
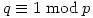 . Let x be an element of order p and y, z have order q. Let
. Let x be an element of order p and y, z have order q. Let 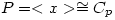 and
and 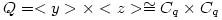 . Â G, H are the semi-direct products of Q by P with
. Â G, H are the semi-direct products of Q by P with - q an odd prime such that
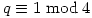 . Let x have order 4 and y, z order q. Let
. Let x have order 4 and y, z order q. Let 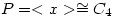 and
and 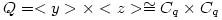 . Â G, H are the semi-direct products of Q by P with
. Â G, H are the semi-direct products of Q by P with
G: Â 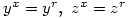 where
where 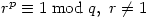
H: Â 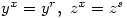 where
where 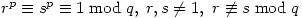 Then G, H are non-isomorphic groups of order
Then G, H are non-isomorphic groups of order 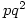 with
with 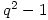 elements of order
elements of order 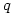 and
and 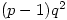 elements of order
elements of order 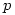 . The smallest such order is
. The smallest such order is 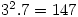
G: Â 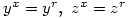
H: Â 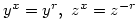 Then G, H are non-isomorphic groups of order
Then G, H are non-isomorphic groups of order 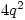 with
with 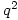 elements of order 2,
elements of order 2, 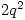 elements of order 4 and
elements of order 4 and 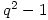 elements of order
elements of order 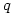 . The smallest such order is
. The smallest such order is 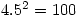 .
.
Norwegian mathematics
Saturday 16 April 2005 at 10:58 pm | In Articles | 7 CommentsI have been teaching Norwegian students for some years; every year it’s a new group but every year they are a pleasure to teach. Since we follow their syllabus the textbook is in Norwegian, which is fine for most mathematics but probability questions can be challenging; just a subtle change in wording can change the resulting probability.
Mathematics is a fairly universal language but there are occasional differences in Norway. In classes for British students I often use . or × for multiplication as in 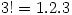 or
or 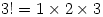 , but Norwegians use · as in
, but Norwegians use · as in 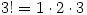 and using the ‘wrong’ notation always produces complaints. Vectors are written as
and using the ‘wrong’ notation always produces complaints. Vectors are written as 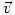 rather than
rather than 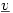 , and the typed bold letter
, and the typed bold letter 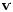 is not used.
is not used.
Other interesting differences in symbols in the textbook are:
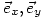 for the unit vectors
for the unit vectors 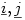
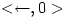 for the interval from
for the interval from 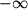 to 0
to 0 In differentiation, function notation is used but I have never before seen it used as in
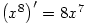 or
or 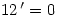
The solution of
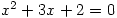 is written
is written 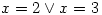
Of course, I am assuming it’s not just the book I’m using, but as the students are comfortable with the notation I expect it’s common in Norway.
The exams are interesting. They are much longer than in the UK lasting 5 hours, so they can only have 1 exam per day. But what is really fascinating, is that to maintain national standards, externally set exams are only sat by selected students, chosen in a lottery. The students only get short notice of whether or not they have been selected and the external exam mark supersedes any internal exam marks. Different selections are made for each subject.
The standard of mathematics they have to learn is roughly equivalent to A level, but the standard of behaviour, willingness to learn and participation is far superior! They study more subjects than is common in the UK and not only do they all know who Niels Henrik Abel was, but even know his most famous result (insolubility of a quintic). Impressive. How many British students can do the same for any British mathematician? They get taught multiplication tables up to 20, which is twice as far as here in the UK and further than the 12 in my day.
Question: Can you name any other famous Norwegian mathematicians? One of them is well known for theorems in group theory. Answers below
Continue reading Norwegian mathematics…
Common Errors
Thursday 7 April 2005 at 5:32 pm | In Articles | 4 CommentsI do sometimes tend to go on and on about common errors students make, such as dividing by zero or assuming what they are trying to prove. The Most Common Errors In Undergraduate Mathematics1 is a long-standing page written by Eric Schechter. It probably contains every error that I’ve ever seen (and more) so should be required reading by all maths students.
A few errors taken at random from the page, hopefully they will encourage you to read it in more detail 🙂
Everything is additive
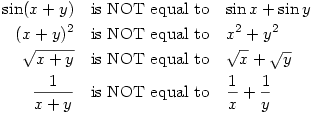
Everything is commutative
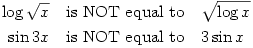
I do like this one, since it gives the right answer via multiple errors
![\displaystyle \int_0^{2\pi}\cos x \;dx=\left[\frac{\sin x}{x}\right]_0^{2\pi}=\frac{\sin 2\pi}{2\pi}-\frac{\sin 0}{0}=\sin - \sin =0 \displaystyle \int_0^{2\pi}\cos x \;dx=\left[\frac{\sin x}{x}\right]_0^{2\pi}=\frac{\sin 2\pi}{2\pi}-\frac{\sin 0}{0}=\sin - \sin =0](/maths/latexrender/pictures/cdd09e0379f65a4920df9e8dcef3be58.gif)
Oh and he has a go at teachers:
- Some teachers are hostile to questions. That is an error made by teachers. Teachers, you will be more comfortable in your job if you try to do it well, and don’t think of your students as the enemy. This means listening to your students and encouraging their questions.
Surely there aren’t many of these type of teachers about are there 😮 ?
1. Undergraduate here is an American term so the page is also highly relevant to A-Level maths students in the UK
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^