Mathematics Weblog
More Trig Ratios
Monday 23 May 2005 at 9:42 pm | In Articles | 6 CommentsStudents studying A level mathematics are expected to know exact values of a few trig ratios such as 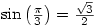 (see Trig Ratios posting). But a visit to Mathworld reveals a whole world of fascinating values.
(see Trig Ratios posting). But a visit to Mathworld reveals a whole world of fascinating values.
Here are just a few of them (you may wish to try proving them)
![\cos\left(\dfrac{\pi}{9}\right)=2^{-\frac{4}{3}}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right) \cos\left(\dfrac{\pi}{9}\right)=2^{-\frac{4}{3}}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right)](/maths/latexrender/pictures/582104b66f6cfb8d988b27f2b7d58ea5.gif)
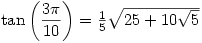
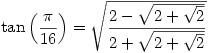
![\sin\left(\dfrac{\pi}{17}\right)=\frac{1}{8}\left[34-2\sqrt{17}-2\sqrt{2}\epsilon^*-2\sqrt{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\epsilon}\:\right]^{\frac{1}{2}} \sin\left(\dfrac{\pi}{17}\right)=\frac{1}{8}\left[34-2\sqrt{17}-2\sqrt{2}\epsilon^*-2\sqrt{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\epsilon}\:\right]^{\frac{1}{2}}](/maths/latexrender/pictures/d96c38bb044f64eab33ac3dacf4b476a.gif)
where 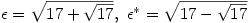
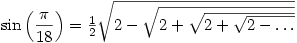 where the sequence of signs
where the sequence of signs 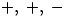 repeats with period 3
repeats with period 3
As I said, fascinating!
Thank goodness  can show these values easily!
can show these values easily!
Simple?? Problem
Sunday 22 May 2005 at 7:13 pm | In Articles | 4 CommentsCan you prove that:
- if you have
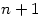 integers less than or equal to
integers less than or equal to 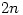 then there are always two of them which are relatively prime?
then there are always two of them which are relatively prime?This problem comes from the biography of Paul Erdös, The Man Who Loved Only Numbers. Erdös posed this problem to Louis Pósa, who was 12 at the time and a child prodigy, and who solved it in about 10 minutes.
This is one of those problems where you can spend hours getting nowhere, and yet the proof is actually very simple 😕
Mathforge
Thursday 12 May 2005 at 9:24 pm | In Articles | Post CommentMathforge is one of the best sites for finding the latest news about mathematics. It reports from what seems like everywhere to tell you what is going on in the world of mathematics. If you are interested in maths then you really should be reading it.
The site uses MathML to show the mathematics so it is good idea to install MathPlayer for Internet Explorer or add maths fonts to Firefox.
PS
Would you believe it? I have just seen that Richard Rusczyk’s the Search for Intelligence Continues. . . blog yesterday recommended Mathforge. I have been meaning to write this post for a week (honest :)) but he got there first.
I Hate Maths
Sunday 1 May 2005 at 1:08 pm | In Articles | Post CommentGooseania has started a discussion at I’m with stupid about why people hate maths (& science) but don’t have the same feelings about the Arts. Can I urge people to contribute to this fascinating topic by posting comments there?
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^