Mathematics Weblog
A Further Five Numbers
Thursday 25 August 2005 at 12:34 pm | In Articles | Post CommentBBC Radio 4 is broadcasting another series of programmes on numbers. This week’s programme features Benford’s Law which says that in naturally occurring data (so not random number tables) the number 1 appears as the first digit around 30% of the time, which is not what one would expect. It is used to detect forgeries.
You can listen to the programme at A Further Five Numbers and the rest of the series will look at 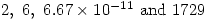
The previous two series are also well-worth listening to; they feature 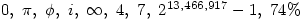 and Game Theory. They can be found at Five Numbers and Another Five Numbers
and Game Theory. They can be found at Five Numbers and Another Five Numbers
(Thanks to Gooseania)
MathWorld
Wednesday 10 August 2005 at 11:47 pm | In Articles | 4 CommentsMathWorld is a wonderful mathematics resource that is well worth browsing. It’s nice to see it has a sense of humour too – see 2001 A Space Odyssey and 42.
Does anybody know of other similar humorous entries at MathWorld or at other such resources such as PlanetMath or the maths pages of Wikipedia?
Odd one out
Wednesday 3 August 2005 at 6:38 pm | In Articles | 5 CommentsYou may well have seen those questions which ask “Which is the odd one out?”, and you often get them as part of a so-called intelligence test 😮
What the question really says is “Which one does the questioner think is the odd one out?”. So it becomes a rather more difficult test of trying to read someone else’s mind and nothing to do with your ability to solve a problem.
Here’s an example of a mathematical “odd one out” to show what I mean. Here are 4 ‘true ‘ statements:
- a. 1 + 1 = 0 true in
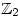 , arithmetic modulo 2
, arithmetic modulo 2b. 1 + 1 = 2 true in
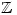 , ring of integers
, ring of integersc. 1 + 1 = 10 true in binary
d. 1 + 1 = 11 true for string concatenation in Basic
The odd one out could be
- b. because it is the only one that is true in
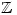
d. because it is the only one that doesn’t involve addition
a. because it is the only one where the right-hand side is less than 1 (using ordering in
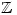 )
)c. because it is the only one where I can’t think of a reason (self-contradictory of course!)
Next time you come across one of those problems, see if you can give a reason why every one of the possibilities could be the odd one out.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^