Mathematics Weblog

Function Notation

Sunday 25 September 2005 at 6:17 pm | In Articles | 9 Comments

The notation 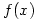is very common and is taught at A level (and sometimes earlier) in the UK. It’s well understood and used but has one well-known flaw – composition of functions. 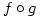or just 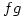is defined by 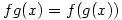. The problem here is that 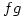means do g first then f, rather than the other way round and is therefore counter-intuitive to the beginner.

One solution is to use a different notation for functions and use 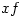instead of 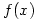. It’s certainly more economical to write but, more importantly, the composite function 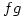is defined by 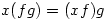, which means do f then g. This seems to be much nicer if it weren’t for one thing. As far as I know, this notation is only taught in advanced courses (3rd year degree/postgraduate) and in books like Universal Algebra by P M Cohn, which is certainly not meant to be read by a novice. By this time, the 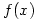is so engrained in a student’s mind it is quite difficult to change to 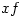– it certainly was for me 😕

Does anyone know if the 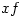notation is taught in more elementary mathematics courses; if so, how was it received?