Mathematics Weblog
Cauchy-Riemann
Friday 28 October 2005 at 2:49 pm | In Articles | 1 CommentThe Cauchy-Riemann equations are one of the first results one comes across in Complex Analysis. A poster on S.O.S. Mathematics Cyberboard has pointed that that proofs like that at Cauchy-Riemann equations tend to take it for granted that if 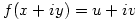 is analytic then the partial derivatives of
is analytic then the partial derivatives of 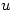 and
and 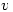 exist. Thus the proof at Cauchy-Riemann equations says
exist. Thus the proof at Cauchy-Riemann equations says
![\displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]} \displaystyle f^{\prime}(z)=\lim_{h\rightarrow 0}{\left[\frac{u(x+h,y)-u(x,y)}{h}+i\frac{v(x+h,y)-v(x,y)}{h}\right]}](/maths/latexrender/pictures/da62bfe56ce08d6df3272c24f9aded5b.gif) and then deduces that
and then deduces that 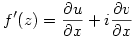
Looking at various textbooks this omission seems to the norm. Even Ahlfors Complex Analysis says: We remark that the existence of the … partial derivatives … is implied by the existence of 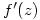
One excellent book A First Course in Complex Functions by G.J.O. Jameson does give a proper proof of this result. It defines differentiability for 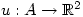 (where
(where 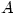 is a subset of
is a subset of 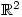 ) at a point
) at a point 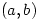 in the interior of
in the interior of 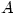 if there exists real numbers
if there exists real numbers 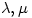 such that, given
such that, given 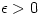 , there exists
, there exists 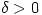 such that, for all real
such that, for all real 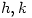 with
with 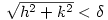 ,
, 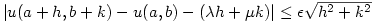
Putting 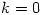 shows that
shows that 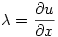 ; similarly
; similarly 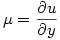
If 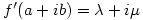 then, given
then, given 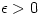 , there exists
, there exists 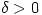 such that for all real
such that for all real 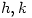 with
with 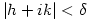
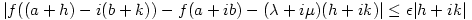
and taking real parts
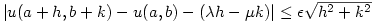 from which it follows that
from which it follows that 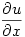 and
and 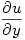 exist. Taking imaginary parts gives the other 2 partial derivatives.
exist. Taking imaginary parts gives the other 2 partial derivatives.
Times
Saturday 22 October 2005 at 9:17 pm | In Articles | 6 CommentsAlong with other British mathematicians I am very lax about how I write the multiplication symbol. I will write
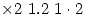
and then maintain that the context will tell the reader what is meant.
The problem comes from the fact that:
1. British students aren’t used to using the dot as a multiplication symbol – it doesn’t seem to be used in schools. They only want to use 
2. The international students have never used  (though it appears on their calculators which seem to be designed for the American market) and they are much more careful with the dot which must be on the centre of the line. They also are unhappy about the British habit of not worrying where the decimal point goes:
(though it appears on their calculators which seem to be designed for the American market) and they are much more careful with the dot which must be on the centre of the line. They also are unhappy about the British habit of not worrying where the decimal point goes: 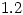 or
or 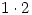
The students love to tell me off for using the ‘wrong’ symbol on the grounds that whatever I do is wrong 😎 It makes for very interesting discussions about the international differences in mathematics and led to a wonderful note from some of the students:
- If I insist on using . for multiplication then asking them to do Q.1 on p.77 should be read as
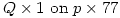 😕
😕 It’s nice to leave a class with a smile on my face.
PS For many years British students have used the word ‘times’ as in times by 3 or even worse ‘timesing’. It sounds horrible to me but I seem to have lost the battle to say ‘multiply’
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^