Mathematics Weblog
Goldbach and Lewis
Tuesday 31 January 2006 at 9:41 pm | In Articles | 1 CommentIt’s not often that mathematics makes an appearance on British TV so I was suprised to see it in Lewis, ITV’s follow up to the Inspector Morse series (see for example Lewis, and the Ghost of Inspector Morse and Newsnight Review).
Oxford University often appeared in the Morse programmes and this time in Lewis it featured a very bright student who had shown that a Fields’ medallist work on the Goldbach Conjecture was flawed, leading to all sorts of murders. Along the way we were shown what a perfect number was, as perfect numbers were used for passwords.
It’s a pity that the mathematics shown on one of the whiteboards was elementary coordinate geometry :). The programme showed how much passion mathematics can arouse, though I wouldn’t have thought it has ever lead to murder!
Mathematics Today Article – Maths Blogs
Monday 30 January 2006 at 12:52 pm | In Articles | Post CommentCraig Laughton, aka Gooseania, has written an article about mathematics blogs in Mathematics Today. Do go to his blog Exploring the blogosphere and read the article and provide the feedback and discussion he asks for.
Cubics
Thursday 26 January 2006 at 9:26 pm | In Articles | 1 CommentA problem that I give some of the students is to show that for a cubic 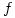 that if
that if 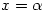 and
and 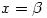 are the x-coordinates of its stationary points then
are the x-coordinates of its stationary points then 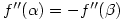 . Hopefully, they will have already noticed this result in the exercises they have done.
. Hopefully, they will have already noticed this result in the exercises they have done.
I then ask them to show that the point of inflexion of 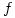 is at the midpoint of the turning points. This involves using the equations for the roots of a quadratic:
is at the midpoint of the turning points. This involves using the equations for the roots of a quadratic: 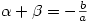 and
and 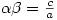 but the algebra isn’t particularly nice (details are here).
but the algebra isn’t particularly nice (details are here).
It dawned on me that there’s a better way which is not only simpler to prove but gives a more powerful result: a cubic is (rotationally) symmetric about its point of inflexion.
To see this, take the cubic and translate it so that the point of inflexion is at the origin. This clearly has no effect on the symmetry so it is sufficient to prove the result in this case.
If 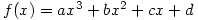 has its point of inflexion at the origin then clearly
has its point of inflexion at the origin then clearly 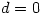 and, as
and, as 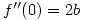 , it follows that
, it follows that 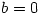 so
so 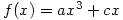 . Rotate this by
. Rotate this by  about the origin, for example by applying the usual matrix
about the origin, for example by applying the usual matrix 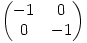 , and you get
, and you get 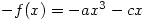 which is clearly the same cubic. Hence it has rotational symmetry about the origin, and in particular, the point of inflexion at the origin is the midpoint of the stationary points.
which is clearly the same cubic. Hence it has rotational symmetry about the origin, and in particular, the point of inflexion at the origin is the midpoint of the stationary points.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^