A Level Exam Questions

Saturday 29 April 2006 at 9:41 pm | In Articles | 6 Comments

At this time of year students are going through past exam questions. It’s tough getting through the AS syllabus in time as the content is very heavy, and to make matters worse, the exam is very early (22nd May). I was somewhat relieved to see (it’s not only me having time problems), and have every sympathy for, Hannah O’Rourke who is an A level student and who writes in this week’s Education Guardian

    … stop and look at your teachers. They’re usually a surprisingly good indicator of whether you should start worrying. If they look calm, cool and collected, relax. My maths A-level exams are coming up in about three weeks and we still haven’t covered three chapters in the textbook, but my teacher’s not panicking, so I’m not panicking … yet.

Revision has highlighted a problem with recent AS papers. Instead of asking you to solve a problem directly the questions take you very slowly though the method required to reach the solution, dividing it up into a number of steps. This suits British students who have been used to answering GCSE questions written in this style. But international students find it confusing, particularly if the exam insists on using a particular method. They are used to being tested for their ability to find the most appropriate method to reach a solution.

Also, one question in a recent paper tells you that 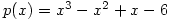p(x)=x^3-x^2+x-6 then asks you to use the Remainder Theorem to find the remainder when 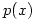p(x) is divided by 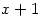x+1. The question is written this way because most British students are not taught long division of polynomials. However, international students usually have a much stronger algebra background and are tempted to use long division to find the remainder. But the examiners say:

    Some candidates clearly did not understand the meaning of the Remainder Theorem or the Factor Theorem and approached each of these by long division. They need to realise that when a particular method is stipulated in the question, any other approach is unacceptable.

I’m really not convinced by this – yes the Remainder Theorem is the easiest and quickest way to find the remainder, but what is wrong with using the (harder) good old long division? That technique should be encouraged.

Calendars

Friday 14 April 2006 at 3:06 pm | In Articles | 2 Comments

It is this time of year that has attracted a lot of attention devoted to finding the dates of religious festivals. A very comprehensive calendar calculator for 25 different calendar systems can be found at Calendrica (Java applet) and details of these systems are given in a fascinating book Calendrical Calculations.

Algorithms to calculate Easter dates have been given by mathematicians through the ages, including Gauss (see for example Mind Over Mathematics: How Gauss Determined The Date of His Birth) but it does produce a few errors. In 1961 the Scottish mathematician T.H. O’Beirne published an algorithm in his Puzzles and Paradoxes column in the New Scientist subsequently reprinted in his book of the same name published by the Oxford University Press (sadly out of print but I throughly recommend looking for a second-hand copy).

O’Beirne’s algorithm (based on an 1876 article in Nature) has the merit of always giving the correct date as well as being easy to use. It is a simple exercise to write a program to do the work for you. Simple Example

O’Beirne’s algorithm
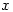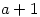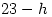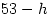The following process gives the date of Easter Sunday as the pth day of the nth month in year x. It also gives the Golden Number a+1 and the epact (23-h or 53-h whichever is between 1 and 30 inclusive). All you have to do is start with the year 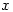x and perform 10 division operations noting the quotients and remainders.

\begin{tabular}{|c|l|r|c|c|} \cline{1-5} \multicolumn{1}{|l|}{Step} & Divide & By & Quotient & Remainder \\ \cline{1-5} 1 & $x$ & 100 & $b$ & $c$ \\ \cline{1-5} 2 & $5b+c$ & 19 & - & $a$ \\ \cline{1-5} 3 & $3(b+25)$ & 4 & $\delta$ & $\epsilon$ \\ \cline{1-5} 4 & $8(b+11)$ & 25 & $\gamma$ & - \\ \cline{1-5} 5 & $19a+\delta-\gamma$ & 30 & - & $h$ \\ \cline{1-5} 6 & $a+11h$ & 319 & $\mu$ & - \\ \cline{1-5} 7 & $60(5-\epsilon)+c$ & 4 & $j$ & $k$ \\ \cline{1-5} 8 & $2j-k-h+\mu$ & 7 & - & $\lambda$ \\ \cline{1-5} 9 & $h-\mu+\lambda+110$ & 30 & $n$ & $q$ \\ \cline{1-5} 10 & $q+5-n$ & 32 & 0 & $p$ \\ \cline{1-5} \end{tabular}
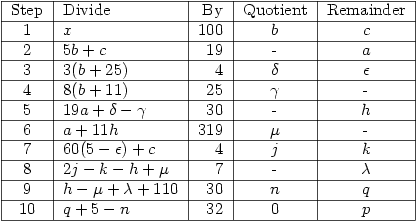
(Table produced by LaTable)

Exam Howlers

Saturday 1 April 2006 at 10:59 pm | In Articles | 3 Comments

Have you any examination howlers? I don’t mean mistakes made by students but errors in the questions themselves, particularly those which make one wonder whether the examiner understands maths as well as they should.

My contribution is an A level question:

    The function 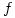f is defined by 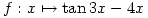\begin{displaymath}f : x\mapsto\tan3x-4x \end {displaymath} and has domain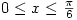 0\le x \le \frac{\pi}{6}

[That can’t be the tan function we all thought we knew]

The next one comes courtesy of Foostyle:

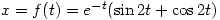    x=f(t)=e^{-t}(\sin 2t+\cos 2t). Show where this crosses the x-axis.

[Are you sure it’s the x-axis you want?]

Your turn …

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^