Mathematics Weblog
Mathematics Under The Microscope
Friday 24 November 2006 at 2:25 pm | In Articles | 2 CommentsMathematics under the Microscope by Alexandre V. Borovik is a new book looking at mathematics, how it works, what happens in the brain when it does mathematics and, using this knowledge, discusses how it should be taught. It is the last part that particularly interests me since so little is understood in this country about mathematical education. We have an ever worsening system of mathematics in schools and colleges for which the blame must lie at the door of those non-mathematicians who think they know how it should be taught. Indeed I refused entry to my classes to anyone who was not a student or who had good mathematics qualifications or who had not read and understood my polemic enough to argue coherently with me about what I had said. There is far too much amateurism in the management of mathematics teaching and today’s Times Higher Education Article Johnson acts to halt closures shows the consequences. I was privileged to be able to teach many international students and it became obvious how far we had fallen behind in this country.
But this article is not supposed to be about my views but to celebrate Mathematics under the Microscope’s contribution to the debate; incidentally it has the important bonus that the author is able to bring to the discussion the benefits of a Russian mathematical education.
It is difficult to convey the scope of the book so I will resort to quoting parts of the author’s overview:
- I look at simple, minute activities, like placing brackets in the sum a + b + c + d + e.
- I analyze everyday observations so routine and self-evident that their mathematical nature usually remains unnoticed: for example, when you fold a sheet of paper, the crease for some reason happens to be a perfect straight line.
- I use palindromes, like MADAM, I’M ADAM, to illustrate how mathematics deals with words composed of symbols—and how it relates the word symmetry of palindromes to the geometric symmetry of solid bodies.
- I even discuss the problem of dividing 10 apples among 5 people!
[…]
In this book, I argue that we cannot seriously discuss mathematical thinking without taking into account the limitations of the information-processing capacity of our brain. In our conscious and totally controlled reasoning we can process about 16 bits per second. In activities related to mathematics this miserable bit rate is further reduced to 12 bits per second in addition of decimal numbers and to 3 bits in counting individual objects. Meanwhile the visual processing module of our brain easily handles 10,000,000 bits per second!
[…]
In my book, I am trying to respond to a sudden surge of interest in mathematics education which can be seen in the mathematical research community. It appears that it has finally dawned on us that we are a dying breed, that the very reproduction of mathematics as a social institution and a professional community is under threat. I approach the problems of mathematical education from this viewpoint which should not be easily set aside: what kind of mathematics teaching allows the production of future professional mathematicians? What is it that makes a mathematician? What are the specific traits which need to be encouraged in a student if we want him or her to
be capable of a rewarding career in mathematics? I hope that my observations and questions might be interesting to all practitioners and theorists of general mathematical education. But I refrain from any critique of, or recommendations for, school mathematics teaching. (my comment: which is a shame!)
[…]
When I read descriptions of some of the experiments in mathematical education, I wanted to call the NSPCC hotline and report child abuse.
[…]
… is a good example of why software based learning of mathematics is intrinsically flawed: the software forces on you a particular mode of visualization. However, visualization is too intimate a component of mathematical thinking to be entrusted to a computer.
To whet your appetite a little more here are a couple of the problems from Chapter 7: What Is It That Makes a Mathematician?
- Find a four-digit number with the following conditions: the product of the extreme digits is equal to 40; the product of the middle digits is 28; the thousands digit is as much less than the units digit as the hundreds digit is less than the tens digit; and if 3, 267 is added to the unknown number, the digits of the number are reversed.
- Here are several dates in Swahili:
tarehe tatu Disemba jumamosi; tarehe pili Aprili jumanne; tarehe nne Aprili jumanne; tarehe tano Octoba jumapili; tarehe tano Octoba jumatatu; tarehe tano Octoba jumatano.
The translations in English are given in random order:
Monday 5 October; Tuesday 2 April; Wednesday 5 October; Sunday 5 October; Saturday 3 December; Tuesday 4 April.
Write in Swahili:
Wednesday 3 April; Sunday 2 December; Monday 1 November.
The book is unusual in that you can download it free under a Creative Commons licence and this also has the advantage that the author can and does update and amend it. Indeed he welcomes comments. Do be aware though that the references are also being updated & renumbered so may get out of synch with a previous version you may have printed out.
The Transcendence of 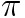
Friday 10 November 2006 at 3:35 pm | In Articles | 9 Comments
Many people have seen the proof that 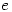 is irrational (eg e is irrational); fewer have read the proof that
is irrational (eg e is irrational); fewer have read the proof that  is irrational (eg Pi is irrational) but how many have seen the proofs that
is irrational (eg Pi is irrational) but how many have seen the proofs that 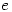 and
and  are transcendental ie not the solution of any polynomial in integer (or rational) coefficients? It’s a shame as these results are fascinating and are easily accessible to degree level students.
are transcendental ie not the solution of any polynomial in integer (or rational) coefficients? It’s a shame as these results are fascinating and are easily accessible to degree level students.
Of course, if you are willing to accept Lindemann’s result that if 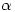 is algebraic then
is algebraic then 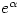 is transcendental, then the fact that
is transcendental, then the fact that  is transcendental follows immediately from the transcendence of
is transcendental follows immediately from the transcendence of 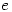 (click on read more below if you can’t see why).
(click on read more below if you can’t see why).
But that’s silly as Lindemann’s theorem is hard to prove. However, I have some notes, typed out on green banda sheets. They were a supplement to a course given by Ian Stewart back in the long forgotten past, well, 1970 to be precise. Very good they are too. I have LaTeXed them and you can read the proofs yourself here: The Transcendence of Pi.
Ian Stewart said (and I agree with him) that back in 1970, a student just needed to understand first-year undergraduate analysis to follow the proofs. I wonder if that is still true?
Continue reading The Transcendence of 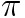 …
…
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^