Mathematics Weblog
Dr Who’s Happy Primes
Saturday 19 May 2007 at 8:34 pm | In Articles | 1 CommentIt’s so nice to see mathematics playing an important part in popular television. In tonight’s Dr Who the spaceship crew had to find the next number in the sequence 313, 331, 367, …. Dr Who recognises this as a sequence of happy primes with the next one being 379. It’s all explained at that Wikipedia article and a longer version of the sequence can be found at the wonderful The On-Line Encyclopedia of Integer Sequences.
It’s interesting that the Dr Who reference was put in the Wikipedia article half-an-hour before the programme was aired so probably an inside job. I was delighted that in the programme Dr Who asked if mathematics was so dumbed down that recreational maths wasn’t studied any more. As Russell T. Davies, the head writer, said in tonight’s Dr Who Confidential, the programme reflects current concerns, so this problem has clearly reached a wider audience than I imagined was the case.
Eigenvalues without determinants
Friday 18 May 2007 at 3:14 pm | In Articles | 9 CommentsMost (all?) undergraduate courses use determinants to introduce eigenvalues and eigenvectors. So the eigenvalues of a matrix 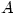 (or linear transformation
(or linear transformation 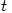 ) are the solutions of
) are the solutions of 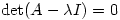 . However, Sheldon Axler published a paper in 1994 called Down with Determinants! where he maintains that determinants should not be used so early in linear algebra courses. He gives a very nice proof of the existence of eigenvalues in finite-dimensional vector spaces (over
. However, Sheldon Axler published a paper in 1994 called Down with Determinants! where he maintains that determinants should not be used so early in linear algebra courses. He gives a very nice proof of the existence of eigenvalues in finite-dimensional vector spaces (over 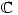 ) which I would like to reproduce here.
) which I would like to reproduce here.
Every linear transformation of a finite-dimensional complex vector space has an eigenvalue.
Here is his proof:
Let 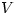 be a non-trivial finite-dimensional complex vector space and t a linear transformation
be a non-trivial finite-dimensional complex vector space and t a linear transformation 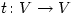 . Let
. Let 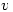 be a fixed non-zero vector in
be a fixed non-zero vector in 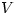 and suppose that
and suppose that 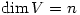 . Then the
. Then the 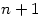 vectors
vectors 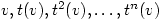 are linearly dependent. Hence there exists complex numbers
are linearly dependent. Hence there exists complex numbers 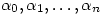 not all 0 such that
not all 0 such that
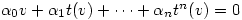 .
.
and hence
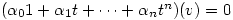 .
.
Now, since 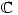 is algebraically closed, Â the polynomial
is algebraically closed, Â the polynomial 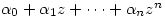 will factorise so we get
will factorise so we get
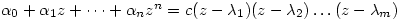 .
.
where  are complex numbers with
are complex numbers with 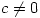 . It follows that
. It follows that
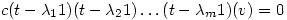
which means that, since this is composition of functions, and 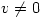 , then
, then
either
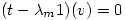 so Â
so  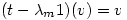  so that
 so that 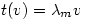 and
and 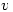 is an eigenvector
is an eigenvector
or
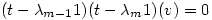 so
so 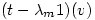 Â is an eigenvector
 is an eigenvector
or
…
or
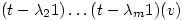 is an eigenvector,
is an eigenvector,
and hence 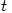 has an eigenvalue. Â Â
has an eigenvalue. Â Â 
Discussion on this approach of not using determinants can be found at NeverEndingBooks and The n-category Café.
Problems, Problems
Saturday 5 May 2007 at 2:22 pm | In Articles | 3 CommentsThe Art of Problem Solving (AopS) site encourages, teaches and promotes mathematics competitions from small local ones right up to the International Mathematical Olympiad (IMO). As it says on its front page:
Is math class too easy for you? Looking for a greater challenge?
You’ve come to the right place.
It has an excellent introduction to  site and a forum to discuss problems. The forum has an RSS feed where students pose new problems every day. So if you’re “looking for a greater challenge” subscribe to this feed. Here is a random sample of some of the problems posed recently, which range from very easy to extremely difficult. Click on the problem number to go to the discussion on it.
site and a forum to discuss problems. The forum has an RSS feed where students pose new problems every day. So if you’re “looking for a greater challenge” subscribe to this feed. Here is a random sample of some of the problems posed recently, which range from very easy to extremely difficult. Click on the problem number to go to the discussion on it.
- 1. We define addition in a different way to usual; an addition statement is true only if the letters in the addends is a rearrangement of the letters in the sum. For example,
10 + 6 = 16?
TEN + SIX = TENSIX = SIXTEN, but to be 16 it would need another E.
Find a “true” addition a + b = c + d.
2. Prove that 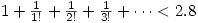 .
3. Let
.
3. Let 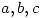 be nonzero real numbers. Find all ordered pairs
be nonzero real numbers. Find all ordered pairs 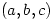 such that
such that 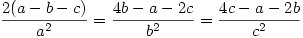 .
.
4. 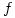 is a continuous complex-valued function satisfying:
is a continuous complex-valued function satisfying:
i) 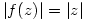
ii) 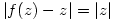
Find 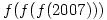
5. If 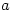 and
and 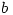 are relatively coprime, find all possible values of
are relatively coprime, find all possible values of 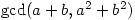 .
.
6. Let 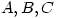 be three angles ofÂ
be three angles of 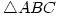 . Prove that
. Prove that 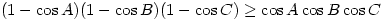 .
.
7. For each function 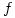 which is defined for all real numbers and satisfies
which is defined for all real numbers and satisfies 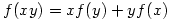 and
and 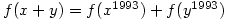 determine the value of
determine the value of  .
.
8. Let 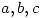 be positive reals such that
be positive reals such that 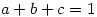 . Prove that
. Prove that 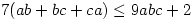 .
.
9. For 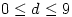 , we define the numbers
, we define the numbers 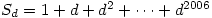 . Find the last digit of the number
. Find the last digit of the number 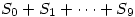 .
.
10. The product of several distinct positive integers is divisible by 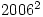 . Determine the minimum value the sum of such numbers can take.
. Determine the minimum value the sum of such numbers can take.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^