Mathematics Weblog
Factorials
Saturday 21 February 2004 at 11:06 pm | In Articles | Post CommentInspired by a test posting on S.O.S. Mathematics CyberBoard
Factorials are fascinating. They are obtained by multiplying the numbers 1, 2, 3, 4, 5 … together and are written using the ! sign. Thus
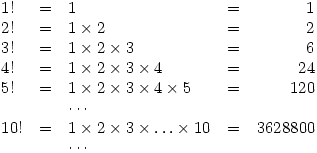
Factorials get large very quickly so 25! = 15 511 210 043 330 985 984 000 000 and as it gets larger there are more and more zeros.
Question: How can you find the number of zeros in 102! without calculating it?
Answer: All you do is count the number of times powers of 5 divide into 102 and add them up. So

Throw away the remainders and we get that there are 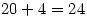 zeros in 102!
zeros in 102!
Now find how many zeros there are in 2004!
Can you show why this method works? Can you generalise it? Have a go, then look for answers on the internet.
Mathematicians will recognise this as a special case of
![\par\boxed{\begin{displaymath}
\textit{The highest power of a prime p dividing n! is }
\sum_{k=1}^\infty \left[\frac{n}{p^k}\right]
\hspace{0.5em}
\end{displaymath}} \par\boxed{\begin{displaymath}
\textit{The highest power of a prime p dividing n! is }
\sum_{k=1}^\infty \left[\frac{n}{p^k}\right]
\hspace{0.5em}
\end{displaymath}}](/maths/latexrender/pictures/a8aa8feb71aa03733c985da6c650a100.gif)
which is not difficult to prove by induction.
More on factorials at mathworld
No Comments yet »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^