Mathematics Weblog
A Level Exam Questions
Saturday 29 April 2006 at 9:41 pm | In Articles | 6 CommentsAt this time of year students are going through past exam questions. It’s tough getting through the AS syllabus in time as the content is very heavy, and to make matters worse, the exam is very early (22nd May). I was somewhat relieved to see (it’s not only me having time problems), and have every sympathy for, Hannah O’Rourke who is an A level student and who writes in this week’s Education Guardian
- … stop and look at your teachers. They’re usually a surprisingly good indicator of whether you should start worrying. If they look calm, cool and collected, relax. My maths A-level exams are coming up in about three weeks and we still haven’t covered three chapters in the textbook, but my teacher’s not panicking, so I’m not panicking … yet.
Revision has highlighted a problem with recent AS papers. Instead of asking you to solve a problem directly the questions take you very slowly though the method required to reach the solution, dividing it up into a number of steps. This suits British students who have been used to answering GCSE questions written in this style. But international students find it confusing, particularly if the exam insists on using a particular method. They are used to being tested for their ability to find the most appropriate method to reach a solution.
Also, one question in a recent paper tells you that 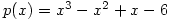 then asks you to use the Remainder Theorem to find the remainder when
then asks you to use the Remainder Theorem to find the remainder when 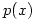 is divided by
is divided by 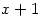 . The question is written this way because most British students are not taught long division of polynomials. However, international students usually have a much stronger algebra background and are tempted to use long division to find the remainder. But the examiners say:
. The question is written this way because most British students are not taught long division of polynomials. However, international students usually have a much stronger algebra background and are tempted to use long division to find the remainder. But the examiners say:
- Some candidates clearly did not understand the meaning of the Remainder Theorem or the Factor Theorem and approached each of these by long division. They need to realise that when a particular method is stipulated in the question, any other approach is unacceptable.
I’m really not convinced by this – yes the Remainder Theorem is the easiest and quickest way to find the remainder, but what is wrong with using the (harder) good old long division? That technique should be encouraged.
6 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
The fault is in the question. Should they want to test knowledge of the remainder theorem, they should pick examples where conceptually simpler methods are poorly suited.
Why not let
p(x) = x^15 – x^2 + x – 6 ?
Comment by jonathan — Sunday 30 April 2006 2:58 pm #
That’s a very good point!
Comment by Steve — Sunday 30 April 2006 3:10 pm #
Maybe one should ask? Why is the teacher behind in AS Maths? And you will find the reason is that students don’t put the effort in and as such the teacher’s time is being wasted. There are problems with attitudes in our country, kids aren’t taught to persevere and if they’re stuck in their homework, they should re-read their notes. Many of them don’t and just say: It’s too hard, I can’t be BOTHERED, I’ll just waste my teacher’s time instead. The problem is of course, when they will be at university or in the work place it doesn’t work like that.
Why give them a surprise when you can tell them at a younger age?
My maths teacher told us in Maths at GCSE (Last year) that we need to persevere, and the strange thing is that not only did our class perform much better than the other one of same level but many people enjoyed it so much they took it for Alevel. (state school)
The syllabus asks that students are aware of the two methods, certainly C2 Edexcel. There is a reason for knowing both methods, and in that case they asked for one. Why do they have two? Well because the remainder theorem can be demonstrated by the definition of polynomial long division. The remainder theorem will be faster and easier to calculate, that’s the entire point of having it in the syllabus. In real life, its a hell of a lot shorter.
“But what’s wrong with the good old division?”
It’s prone to error, but I agree that AS students should be able to do it and it should be asked sometimes as an alternative to the remainder theorem.
It also gives a little insight in Higher level Arithmetic.
I agree with Jonathan they could have put a higher degree polynomial.
(A2 Maths student)
Comment by Aaron — Friday 5 May 2006 8:04 pm #
I remember Richard Feynman making the comment that it was an absolute absurdity to prescribe a method for solving a problem. “In real life it doesn’t matter how you do it, so long as you can do it” was roughly how he put it. And I agree with him.
Comment by Philip — Wednesday 21 June 2006 2:46 pm #
I can only paraphrase Richard Feynman:
“I always new that our system of mathematical education sick. Today I was told that this is cancer.”
Comment by Alexandre Borovik — Saturday 23 September 2006 11:42 am #
[…] The question just asks you to find the x-coordinate of the minimum point of using an iterative solution of . Of course it holds your hand through the question, as is the fashion these days as I have mentioned before. […]
Pingback by Mathematics Weblog » A Level Results Day — Sunday 6 May 2007 10:32 pm #