Mathematics Weblog
More on Maths Teaching in HE
Monday 31 July 2006 at 9:24 pm | In Articles | 1 CommentThanks to Gooseania for bringing to my attention a couple of interesting papers on teaching mathematics in US universities.
1. Teaching at the University Level by Steven Zucker explains how the student grading of course teaching can lead to dumbing down of courses. The teacher tends to please the student at the expense of covering the difficult parts of the mathematics course. The author believes that it would help greatly if students were to be told on arrival at university the huge difference in what is expected of them as compared to the schools they have just left.
It is unfortunate that in the UK it is so difficult to persuade non-mathematical teaching experts (so-called) that maths is hard and that I don’t expect students to understand it first-time round, which is why I spend so much time at the end of an A level course revising everything. It is true that at A level and beyond few students really understand the mathematics they have been taught until a year later (and after the exams) when they have to use it and suddenly the mist clears. I well remember looking back on a tough measure theory course that I didn’t really understand at the time, thinking ‘oh it’s obvious now’. It’s a natural part of learning mathematics and should be accepted as such.
2. Teaching Mathematics Graduate Students How to Teach by Solomon Friedberg is a paper on the usefulness of mathematical case studies for new university teachers who haven’t got the experience to judge how to pitch their courses. He gives a case study where a student argues that he should have got full marks in the following exam question (the italics are mine):
- Let
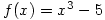 . Use the definition of the derivative to compute the slope of the tangent line to the graph of
. Use the definition of the derivative to compute the slope of the tangent line to the graph of 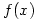 at the point where
at the point where 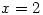 .
.The student questions why his answer only scores 5 marks out of 20. His answer was:
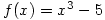 ,
, 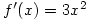 .
. 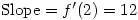 .
.The teacher fails to persuade the student of the importance of the method asked for.
Reading the question carefully and doing exactly what is asked for is a skill I have always taught A level and University students. Sometimes I even resort to “mathematics is not a democracy – you have to do as you are told” 🙂
1 Comment »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
“Reading the question carefully and doing exactly what is asked for is a skill I have always taught A level and University students. Sometimes I even resort to “mathematics is not a democracy – you have to do as you are told””
Indeed it doesn’t work as a democracy and consequently the limit definition does not necessarily explain why the rule for differentiation works. One might use non-standard analysis to explain why the derivative of 3x^2 equals 6x. There also exists the problem of how we can factor out h in
lim h->0 f(x+h)-f(x)/h, when h/h actually means 0/0…. I repeat h/h means 0/0, which we don’t allow by definition in mathematics. e.g. take the limit as h approaches 0 of x^2. We have lim h->0 f(x+h)-f(x)/h. So we get lim h->0 (x+h)^2-x^2/h.
lim h->0 (x^2+2hx+h^2)-x^2/h. This equals lim h->0 2hx+h^2/h. Remember, the limit of h as it approaches 0 equals 0. Now you want to say that 2hx+h^2/h equals 2x+h. But, 0/0 ISN’T DEFINED. If you replace h by delta x, delta x isn’t defined.
Now we could define delta x, or h, by saying that it belongs to the open interval (0, infinity) or that it belongs to the open interval (-infinity, 0). But, then we don’t know the behavior of h at exactly 0. We only know the behavior of h at approximately 0 at best. So, we can’t evaluate the rate of change exactly at 0, we can only evaluate what WOULD BE the rate of change at 0 WERE we to have a constant change throughout our entire function. Consequently, ‘the professor’s’ argument here about using the definition of a derivative has no more weight than the student’s, because his method doesn’t stick to definitions by saying that 0/0 has a definition. Additionally, the professor says we have exact knowledge of that derivative (the student’s answer) when we actually only have a WHERE-WOULD condition. In plainer language we just have a hypothesis.
Additionally, this doesn’t accord with how many mathematicians actually operate on a day-to-day basis as mathematicians. A good theorem, and sometimes even a mere proposition, becomes a definition. Euclid does this in his elements by using previous demonstrated propositions to deduce other propositions. A lemma also does something similar by changing a proposition into a definition for the next proposition. In other words, a lemma changes from a demonstrated proposition to a definition with respect to the next proposition. Once you’ve seen the limit definition and how it works, the rule nx^(n-1) works as a definition (or at least an operational definition) for many problems.
Comment by Doug Lefelhocz — Wednesday 9 August 2006 2:59 pm #