Mathematics Weblog
The Transcendence of 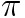
Friday 10 November 2006 at 3:35 pm | In Articles | 9 Comments
Many people have seen the proof that 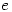 is irrational (eg e is irrational); fewer have read the proof that
is irrational (eg e is irrational); fewer have read the proof that  is irrational (eg Pi is irrational) but how many have seen the proofs that
is irrational (eg Pi is irrational) but how many have seen the proofs that 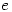 and
and  are transcendental ie not the solution of any polynomial in integer (or rational) coefficients? It’s a shame as these results are fascinating and are easily accessible to degree level students.
are transcendental ie not the solution of any polynomial in integer (or rational) coefficients? It’s a shame as these results are fascinating and are easily accessible to degree level students.
Of course, if you are willing to accept Lindemann’s result that if 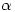 is algebraic then
is algebraic then 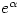 is transcendental, then the fact that
is transcendental, then the fact that  is transcendental follows immediately from the transcendence of
is transcendental follows immediately from the transcendence of 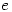 (click on read more below if you can’t see why).
(click on read more below if you can’t see why).
But that’s silly as Lindemann’s theorem is hard to prove. However, I have some notes, typed out on green banda sheets. They were a supplement to a course given by Ian Stewart back in the long forgotten past, well, 1970 to be precise. Very good they are too. I have LaTeXed them and you can read the proofs yourself here: The Transcendence of Pi.
Ian Stewart said (and I agree with him) that back in 1970, a student just needed to understand first-year undergraduate analysis to follow the proofs. I wonder if that is still true?
If  were algebraic then so would
were algebraic then so would 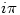 be. It would follow from Lindemann that
be. It would follow from Lindemann that 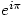 is transcendental which is silly. So
is transcendental which is silly. So  must be transcendental.
must be transcendental.
9 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Are you using the G-F theorem with a=e (*) and b=i*pi (in combination with “the most remarkable equation in mathematics” (C) R Feynman]) to get a contradiction, and so deducing that i*pi, and hence pi, cannot be algebraic? But G-F requires both a and b to be algebraic, so (*) is not allowed. Or have I misunderstood/misrepresented your argument?
Comment by Rob Mitchell — Friday 17 November 2006 2:30 pm #
Whoops! Memory plays some strange tricks – I could have sworn that Gelfond-Schneider was the theorem behind the proof when I first saw it in a seminar long, long ago. Clearly it couldn’t have been. It must instead have been a result like Lindemann’s that showed that if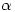 is algebraic then
is algebraic then 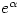 is transcendental.
is transcendental.
Thanks for pointing that out and I’ve changed the post accordingly.
Comment by Steve — Friday 17 November 2006 3:00 pm #
Pi = 3.14159265
Comment by math — Thursday 7 December 2006 9:39 pm #
I don’t think what Ian Stewart said is true anymore! (well not in my case anyway!) It’s easy to blame schools and colleges about the standards of maths teaching (so I will blame them!) but what can one do whilst at Universtiy to overcome this?
Comment by shazmania — Wednesday 31 January 2007 3:37 pm #
You are the victim so it’s difficult for you to catch up. I suppose you could ask your lecturers what extra reading you could do, though I do not underestimate the difficulty in doing this on your own.
Another place to ask is on Gooseania’s blog. He is a maths postgrad at Manchester Uni who helps undergraduate students – maybe he, or his students, will have ideas.
Comment by Steve — Wednesday 31 January 2007 4:14 pm #
yes, it is pretty difficult since you’re thrown into the deep end straight away. I have been browsing some universities reading list and have got a few books from the library (like Polya) but it’s not an easy task. I have tried asking my lecturers and the response I mostly receive is that go to the library and see which book you like!!
tbh I was pretty shocked to learn that Ian Stewart is a maths professor in the UK! (I’m currenlt reading his book Maths:the science of patterns! and always thought he was American!)
I do tend to ask on Goosenia, but there I felt that undergraduate students, amidst the post grads are seen as wierdos (so to speak)!! Anyway, thanks for the advice. University emphasises more on what one can do for themselves, rather than the other way round. Just need to get out of college and spoon-feeding mode!
(yes, I like blaming others! :p )
Comment by shazmania — Wednesday 31 January 2007 5:27 pm #
aaaah, I must apologise, the author of Mathematics: The science of patterns is Keith Delvin not Ian Stewart! The book by Ian Stewart which I had was ‘The Foundation of mathematics!’ 😮
Comment by shazmania — Wednesday 31 January 2007 6:14 pm #
Keith Devlin is also British though he emigrated to America some years ago. He used to write a maths column in the Guardian in the seventies.
Ian Stewart has been at Warwick University since the late sixties when he was a postgrad. My claim to fame is that I was a student there at the same time and I have a copy of his PhD thesis “Subideals of Lie Algebras”. It is 170+ pages manually typed on quarto paper.
Comment by Steve — Wednesday 31 January 2007 6:31 pm #
[…] é transcendental. Vale a pena estudar. Envolve um pouco de cálculo diferencial e integral. Veja o Mathematics Weblog ou diretamente o arquivo em pdf. Ao demonstrar que pi é transcendental, fica fácil mostrar que o […]
Pingback by Comentários, CrÃticas, Dicas etc» Blog Archive » Irracionais e transcendentais: π & e — Saturday 8 September 2007 2:34 am #