Mathematics Weblog
Problems, Problems
Saturday 5 May 2007 at 2:22 pm | In Articles | 3 CommentsThe Art of Problem Solving (AopS) site encourages, teaches and promotes mathematics competitions from small local ones right up to the International Mathematical Olympiad (IMO). As it says on its front page:
Is math class too easy for you? Looking for a greater challenge?
You’ve come to the right place.
It has an excellent introduction to  site and a forum to discuss problems. The forum has an RSS feed where students pose new problems every day. So if you’re “looking for a greater challenge” subscribe to this feed. Here is a random sample of some of the problems posed recently, which range from very easy to extremely difficult. Click on the problem number to go to the discussion on it.
site and a forum to discuss problems. The forum has an RSS feed where students pose new problems every day. So if you’re “looking for a greater challenge” subscribe to this feed. Here is a random sample of some of the problems posed recently, which range from very easy to extremely difficult. Click on the problem number to go to the discussion on it.
- 1. We define addition in a different way to usual; an addition statement is true only if the letters in the addends is a rearrangement of the letters in the sum. For example,
10 + 6 = 16?
TEN + SIX = TENSIX = SIXTEN, but to be 16 it would need another E.
Find a “true” addition a + b = c + d.
2. Prove that 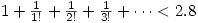 .
3. Let
.
3. Let 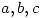 be nonzero real numbers. Find all ordered pairs
be nonzero real numbers. Find all ordered pairs 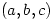 such that
such that 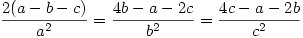 .
.
4. 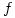 is a continuous complex-valued function satisfying:
is a continuous complex-valued function satisfying:
i) 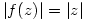
ii) 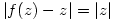
Find 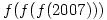
5. If 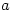 and
and 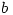 are relatively coprime, find all possible values of
are relatively coprime, find all possible values of 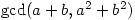 .
.
6. Let 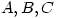 be three angles ofÂ
be three angles of 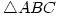 . Prove that
. Prove that 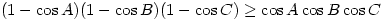 .
.
7. For each function 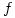 which is defined for all real numbers and satisfies
which is defined for all real numbers and satisfies 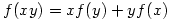 and
and 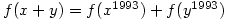 determine the value of
determine the value of  .
.
8. Let 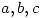 be positive reals such that
be positive reals such that 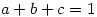 . Prove that
. Prove that 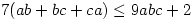 .
.
9. For 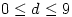 , we define the numbers
, we define the numbers 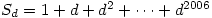 . Find the last digit of the number
. Find the last digit of the number 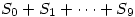 .
.
10. The product of several distinct positive integers is divisible by 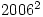 . Determine the minimum value the sum of such numbers can take.
. Determine the minimum value the sum of such numbers can take.
3 Comments
Sorry, the comment form is closed at this time.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Another similar site is http://www.zadania.info Unfortunately it is in Polish only.
Comment by jan — Monday 23 June 2008 9:20 am #
art of problem solving is fantastic. It contains so many challenging math problems. Another good thing is that it is linked to http://www.mathlinks.ro, which have even more hard problems.
Comment by Dave S — Friday 27 June 2008 11:31 am #
They are the same sites, just different skins.
Comment by steve — Friday 27 June 2008 12:15 pm #