Mathematics Weblog
Trig Ratios
Sunday 4 April 2004 at 10:55 am | In Articles | 1 CommentA level syllabuses these days expect you to remember the exact values of sin cos and tan of certain angles. 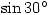 is easy enough as the calculator will give you the exact answer, but unless you know roughly what
is easy enough as the calculator will give you the exact answer, but unless you know roughly what 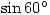 should be then the calculator will be no help.
should be then the calculator will be no help.
But, help is at hand 😀 Memorising formulae is easier when there’s a pattern and the following table gives such a pattern.
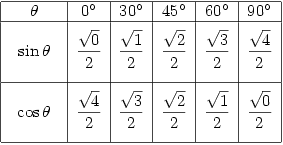
Isn’t that amazing! I only came across this a few years ago but apparently it’s been around at least since the 1950’s.
What about tan? Since 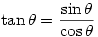 you just divide a value from the second row by the one below it (but please not for
you just divide a value from the second row by the one below it (but please not for 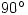 ; see Tuesday 16 March).
; see Tuesday 16 March).
1 Comment »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Thank you! I had an instructor demo this once and I wrote it down but promptly lost it. I’ve been looking for it again for months.
Comment by Jakob — Tuesday 24 May 2005 8:46 am #