Mathematics Weblog
This site uses LatexRender for the mathematics
General Comments
Saturday 1 March 2003 at 2:12 pm | In Articles | 143 CommentsThis is where you can post general comments
143 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
I didn’t buy that second Riebenboim book. Didn’t have another £30. Also the reason for wanting it disappeared. I make an educated guess that Wieferich was able to prove FLT case 1 unless two of X;Y;-Z; were equal mod p. Certainly if that is the case the Wieferich condition follows. But using another piece of work from an old number theory book over a hundred years old, the Wieferich condition could have been extended to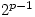 =1 mod
=1 mod 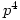 (if my guess is correct). Vandiver got close with that condition but included an ‘or’ condition, but a single condition suffices.(if my guess is correct). For the Wieferich condition Fermat was able to prove
(if my guess is correct). Vandiver got close with that condition but included an ‘or’ condition, but a single condition suffices.(if my guess is correct). For the Wieferich condition Fermat was able to prove 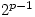 =1 mod
=1 mod 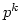 for all positive integers k. In fact, regardless of the Wieferich condition, he could prove that for X;Y; prime to p for the Fermat equation to have a solution,
for all positive integers k. In fact, regardless of the Wieferich condition, he could prove that for X;Y; prime to p for the Fermat equation to have a solution, 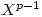 =
= 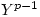 mod
mod 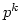 for all integers k. Proof to be published this year. 🙂
for all integers k. Proof to be published this year. 🙂
Do you know if that was the condition Wieferich couldn’t handle?
Comment by Oliver — Wednesday 15 April 2009 1:35 pm #
No sorry I don’t.
Comment by Steve — Wednesday 15 April 2009 1:49 pm #
Thanks for the response Steve. It irks me somewhat that I can’t find a copy of Wieferich’s limited proof on the net (for free!), but it is hidden away in some subscription mathematical journal. With the copyright around these things I would even hazard a guess that Riebenboim’s book doesn’t even detail the exact Wieferich argument but talks around it.
Changed days from Archimedes running down the street naked shouting ‘Eureka’ 🙂
Comment by Oliver — Wednesday 15 April 2009 3:13 pm #
So, any takers on this one? If you take as a given what I say Fermat could prove in post 101, how do you extend that to him proving no integer solutions to his problem existed for both case 1 and case 2?
Comment by Oliver — Friday 17 April 2009 6:04 pm #
Steve, can you possibly direct me to a professor of number theory with an open enough mind to spend 10 minutes reading a one and a half page paper on FLT. I get the feeling that none of them will touch it with a barge pole.:-(
Comment by Oliver — Tuesday 21 April 2009 10:48 am #
or alternatively give me contact details if you are prepared to review it yourself
Comment by Oliver — Tuesday 21 April 2009 1:01 pm #
Looks like I’m talking to myself here Steve.
I’ll post the answer to 104 for case 1 on Monday if nobody else does.
Comment by Oliver — Friday 24 April 2009 8:57 pm #
It has been published that in any solution to FLT case 1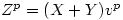 , so given 101 we can continue
, so given 101 we can continue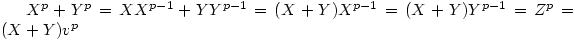 mod
mod 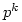 for all k.
for all k.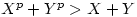 for positive integers unless X;Y; = 1 (and 2 is not the
for positive integers unless X;Y; = 1 (and 2 is not the 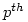 power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
?
?if X;Y; are finite X;Y;Z; have a common factor, v
v ? 1 as
So all that is needed is to prove the given in 101. Anybody want to finish off the case 2 with the given in 101?
Comment by Oliver — Monday 27 April 2009 1:01 pm #
Is there a definition anywhere of what symbols you can use. I used ‘therefore’ special character and ‘not equal’ special character, and they have come out ?
Comment by Oliver — Monday 27 April 2009 1:04 pm #
ignore that last post, I’ve found them on equation editor
Comment by Oliver — Monday 27 April 2009 1:15 pm #
It has been published that in any solution to FLT case 1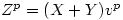 , so given 101 we can continue
, so given 101 we can continue
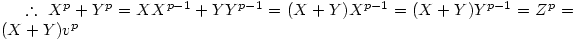 mod
mod 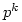 for all k.
for all k.
 if X;Y; are finite X;Y;Z; have a common factor, v
if X;Y; are finite X;Y;Z; have a common factor, v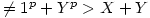 for positive integers unless X;Y; = 1 (and 2 is not the
for positive integers unless X;Y; = 1 (and 2 is not the 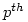 power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
v
So all that is needed is to prove the given in 101. Anybody want to finish off the case 2 with the given in 101?
Comment by Oliver — Monday 27 April 2009 1:23 pm #
It has been published that in any solution to FLT case 1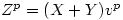 , so given 101 we can continue
, so given 101 we can continue
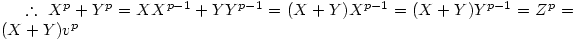 mod
mod 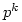 for all k.
for all k.
 if X;Y; are finite X;Y;Z; have a common factor, v
if X;Y; are finite X;Y;Z; have a common factor, v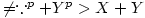 for positive integers unless X;Y; = 1 (and 2 is not the
for positive integers unless X;Y; = 1 (and 2 is not the 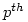 power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
v
So all that is needed is to prove the given in 101. Anybody want to finish off the case 2 with the given in 101?
Comment by Oliver — Monday 27 April 2009 1:25 pm #
sorry Steve.
Comment by Oliver — Monday 27 April 2009 1:26 pm #
It has been published that in any solution to FLT case 1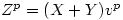 , so given 101 we can continue
, so given 101 we can continue
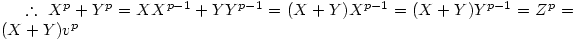 mod
mod 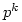 for all k.
for all k.
 if X;Y; are finite X;Y;Z; have a common factor, v
if X;Y; are finite X;Y;Z; have a common factor, v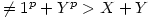 for positive integers unless X;Y; = 1 (and 2 is not the
for positive integers unless X;Y; = 1 (and 2 is not the 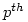 power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
v
So all that is needed is to prove the given in 101. Anybody want to finish off the case 2 with the given in 101?
Comment by Oliver — Monday 27 April 2009 1:31 pm #
Is there any practice site you can practise posting the finished article with the tex statements in it?
Comment by Oliver — Monday 27 April 2009 1:32 pm #
There are lots. See Online LaTeX. The first list is for fragments, the second list is for complete documents.
Comment by Steve — Monday 27 April 2009 1:49 pm #
It has been published that in any solution to FLT case 1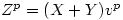 , so given 101 we can continue
, so given 101 we can continue
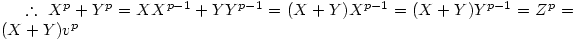 mod
mod 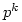 for all k.
for all k.
 if X;Y; are finite X;Y;Z; have a common factor, v
if X;Y; are finite X;Y;Z; have a common factor, v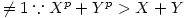 for positive integers unless X;Y; = 1 (and 2 is not the
for positive integers unless X;Y; = 1 (and 2 is not the 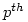 power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
power of a positive integer). This is a contradiction as X;Y;Z; are co-prime.
v
Comment by Oliver — Monday 27 April 2009 2:34 pm #
I suggest you get your own (free) WordPress blog at http://wordpress.com/ which has LaTeX support, then you can write and edit your own articles there.
Comment by Steve — Monday 27 April 2009 2:49 pm #
ok Steve I’ll do that. Sorry if I’ve caused any problem. You’ve been very helpful. Can I still request info here? e.g. Do you know if Euler’s proof of Fermat’s prime theorem is available on the net?
i.e. the one that each prime can be expressed as the sum of 2 squares. Google doesn’t seem to find it.
Comment by Oliver — Monday 27 April 2009 3:49 pm #
Euler’s proof by infinite descent
Comment by Steve — Monday 27 April 2009 5:23 pm #
Superb Steve, many thanks.
Comment by Oliver — Monday 27 April 2009 5:37 pm #
I am wondering whether a professional mathematician would find my amateur’s way of expressing something confusing.
I have a multipliication group. I have 3 members A1;A2;A3;
The A members have a special property.
I have a sub group S and a member s of that sub group.
Is the following statement clear.
Define the As coset as the set of 3 A members multiplied in turn by s
The reason I ask is that coset is normally used when multiplying a sub group by a member of the group, so I’m wondering if that could lead to confusion.
The set A happens to be a sub group, but I don’t particularly want to prove that.
Comment by Oliver — Saturday 25 July 2009 9:13 am #
I see the word ‘partition’ is used sometimes in describing things like these cosets.
I’m looking for a verb. I have a set of pairs which have a common property. Each pair relates 1:1 to another set of pairs which have a second common property.
I wish to say each first pair ‘ ‘ which second pair is used to form the second property.
I’ve rejected ‘mandates’; ‘dictates’ and at the moment have ‘prescribes’ as my best choice. Any suggestions welcomed.
Comment by Oliver — Monday 5 October 2009 2:32 pm #
Any comments on the use in a mathemaical proof of three dots, meaning ‘therefore’, and an upside down three dots, meaning ‘because’?
I’m told ths usage is now ‘frowned upon’.
Comment by Oliver — Sunday 15 November 2009 4:05 pm #
What is the preferred (if any) mathematical way of expressing a congruence? After the Gaussian congruence symbol should you say,
mod p or (mod p)?
I have come across people that use both.
Comment by Oliver — Sunday 6 December 2009 4:38 pm #
Either will do though a publisher might have a preference.
Comment by Steve — Sunday 6 December 2009 6:03 pm #
thanks Steve. Given that the less ink on paper,the better, I’ve removed the parentheses from around the mod p. I’ll worry about a publisher after I find somebody to read the paper.
🙂
Comment by Oliver — Tuesday 8 December 2009 2:21 am #
I have a commutative ring. I can produce the value of a term A.(B+C) in two different ways.
Multiplying the second way by unity, in the form of F multiplied by the inverse of F, I obtain a term A.(D+E), which obviously is the same value as A.(B+C). I think I can say that either B=D and C=E, or B=E and C=D, i.e. the terms being added cannot be B + delta, and C – delta (unless of course B+delta = C). Would you agree? I have an alternative way of explaining what I’m about, but this one is more succinct.
Comment by Oliver — Thursday 14 January 2010 3:22 pm #
Unless you have division ring you can’t even say D+E=B+C. Even if that were true then you can’t say anything more eg in the ring of integers 1+3=2+2.
Comment by Steve — Thursday 14 January 2010 4:11 pm #
Having failed in my global attempts to get a review of my paper, I’m looking to submit it to be refereed. Is my understanding of this correct?
You submit a paper. If it is accepted for publication, you are asked to transfer the copyright. It is published in a journal. Only subscribers to the journal can read it, and have to pay a subscription. A bit like the Wieferich situation above.
You can make it open access, but you yourself pay a fee. In both cases, you do not own the copyright, and cannot do things like putting it on the web for all to see.
Comment by Oliver — Saturday 13 February 2010 11:39 am #
Two requests Steve.
1. I’m writing a book. Can I include some of your posts above in it?
2. I submitted my paper to the Glasgow mathematical journal. More than two weeks later it still hadn’t been assigned to anybody. I spoke with the editor, who confirmed that if it was accepted it couldn’t also be published on the internet, so we agreed to withdraw the paper. Any chance of an informal review from you before I put it on the net?
Comment by Oliver — Tuesday 9 March 2010 9:45 am #
I lack your precision in 129 Steve.
Taking the ring of integers, and a member formed by A.(b+c). A fixed and non zero. b;c; allowed to vary, but their sum kept constant. This sum may be zero. There are an infinite number of solutions for any A and any b+c.
Is the following precise?.
Each factorisation is unique as A is fixed, and no b+c can be factorised into another b+c.
If precise, does that hold for b+c=0?
Comment by Oliver — Tuesday 16 March 2010 9:36 am #
One last question and I’m off. The residues of the ring of integers mod p^2 form a ring wrt modular multiplication and addition mod p^2. I’m interested in the factors of 0.
If I take a,b, prime to p and a+b congruent to 0 mod p^2, and I take p.(c+d) congruent to 0 mod p^2 where c+d is congruent to zero mod p but not zero mod p^2, it is correct to say, isn’t it, that a+b cannot factorise to p.(c+d) because a:b: are prime to p?
Comment by Oliver — Tuesday 6 April 2010 1:11 pm #
Any a, b prime to p with a+b=18, p=3, any c,d with c+d=6. Then a+b=p(c+d).
Generally, if a+b=0 mod p^2 then obviously a+b=p.k with p dividing k. Now let c+d=k. If p^3 doesn’t divide a+b then p^2 won’t divide c+d.
Comment by Steve — Tuesday 6 April 2010 7:30 pm #
I’m dealing with residues, Steve, so with p=3, they are all less than 9. With a=2, b=7, a+b = 0 mod 9. With c=1, d=5, 3(c+d) = 0 mod 9.
What I’m trying to say is that I can’t factorise the elements a:b: so that they become 3(c+d). I can express their sum as that, but to me that is not factorising the elements. I can factorise a+b as 2(1+8), 4(5+4), 8(7+2), mod 9 etc. but not as 3(1+5).
And the reason is that the residues are prime to 3. Does this make sense?
Comment by Oliver — Wednesday 7 April 2010 12:48 am #
If 0<a,b<p2 and a+b=0 mod p2 then a+b=p2 so a+b=p.p and hence c+d=p.
So eg (2+7)=3(1+2) answers the original question.
Comment by Steve — Wednesday 7 April 2010 11:55 am #
That’s a bit of a blow Steve. You are saying that a+b can factorise as p.p even though both a and b are prime to p. And don’t you have division by a factor of zero when you say hence c+d=p? I’ll leave it there. Thanks for your response.
Comment by Oliver — Wednesday 7 April 2010 12:57 pm #
I think I’ve cracked it Steve. I have a certain type (class) of factor a+b,a:b: prime to p, which may be zero at some modular level, but eventually has to be non zero. Dealing at mod p^2 level above I cannot make my conclusion. The answer is to deal at mod p^3 level. From an a+b zero factor mod p^3 I have to derive other a+b type factors, either 0 or of form p(a+b). Analysing these factors mod p^2 it can only be that a+b = 0 mod p^2, which is enough for my problem.
Comment by Oliver — Thursday 8 April 2010 12:28 pm #
Needless to say I cannot say a+b is zero mod p^3, so that is not the answer.
My last effort is as follows.
I form a+b residues mod p^2 on a 1:1 basis from other residues mod p^2. I end up with 10 say mod p^2. 5 of them don’t add to zero and can be rejected. The other 5 add to zero and are formed by adding two residues mod p^2. I can factor these as p.(a+b) where a+b is one of the rejected a+b pairs.
Since I am not factorising an integer, but a residues sum, I contend that the (a+b) factor in p.(a+b) is a residue mod p. I cannot make it an (a+b) residue mod p^2, and therefore I maintain my 1:1 relationship with a+b mod p^2.
Comment by Oliver — Friday 16 April 2010 8:18 am #
Ignore the last paragraph above. What remains is my argument. (a+b) can only be zero. I don’t want to get into Dr. Faustus and the devil, but in dealing with the devil in mathematics he has two very powerful weapons, infinity and zero. I managed to control infinity, but zero almost beat me. Thanks for being able to bounce ideas off you. Over and out.
Comment by Oliver — Thursday 22 April 2010 4:51 pm #
After a marriage and a major house refurbishment I’m back to finish off my problem.
Having claimed victory over the devil, I find myself amusingly playing devil’s advocate to try and find a flaw in my paper. The binomial theorem works for negative integers. Does it work when one of the integers is 0?
My problem is to analyse the sum of two pth powers of integers, p an odd prime. We will do it with residues of these integers modulo p^k. The integers :a:b: are prime to p, but their sum has a factor p, and possibly a facot with higher powers of p.
One stratagem generally employed is to express
the sum as ((a+b)-b)^p +b^p and expand out the first term with the binomial theorem. The b^p terms cancel out leaving a factored expression (a+b)() and you prove the () factor has a single factor p.
Now I can prove what a and b must be for all the various combinations, but my factorisation is of the form (a+b)() where () does not have the factor p. The devil points this out, but I reply I can take my solution :a:b: mod p^k and exponentiate it using the stratagem and the result will be a residue expression mod p^k of (a+b)p(). Is this also valid if a+b=0 mod p^k, i.e. the stratagem forms (0)p() mod p^k? If not, I need to add another section.
Comment by Oliver — Thursday 27 January 2011 1:50 pm #
Forget that question Steve. It looks like the binomial theorem for (a+b)^p will handle any type of value ( that I can think of) for a and b, including (cosx+sinx). I am thefore taking it that I can create my factorisation when a+b add to zero.
Comment by Oliver — Thursday 27 January 2011 5:15 pm #
As I see it, the set of residues of integers mod p^k, k a positive integer, meet the wikipedia criteria to form a commutative ring under residue addition and multiplication mod p^k.
I want to know if this set is a field.
For a ring to be a field, Wikipedia defines the requirement that every non zero element be invertible. In this set, every element that is not a factor of zero is invertible, so it is slightly different from the wikipedia requirement.
Comment by Oliver — Wednesday 13 April 2011 1:07 pm #