Mathematics Weblog
This site uses LatexRender for the mathematics
Cancelling
Tuesday 20 April 2004 at 4:27 pm | In Articles | 1 CommentStudents love to cancel wherever they can, so much so that the book Comic Sections (now out of print) had the following joke:
- The student law of universal cancellation: If the same symbol x occurs in any two different places on the one page it may be cancelled
So you get horrors like  😮
😮
And yet strange things can happen. It is true that 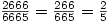 .
.
What is remarkable is that you can have as many sixes as you like and cancel them as many times as you like so, for example, 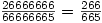 . Can you prove this is true? Can you find 3 other similar fractions?
. Can you prove this is true? Can you find 3 other similar fractions?
1 Comment »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
my math teacher in high school went over the same idea of canceling versus reducing often.
He used the example 16/64 and 64/16. Without the 6s, it makes a true statement.
Comment by chris — Saturday 18 September 2004 3:35 am #