Mathematics Weblog
This site uses LatexRender for the mathematics
Problem
Monday 26 April 2004 at 4:53 pm | In Articles | 4 CommentsFirstly, show that:
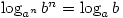
Secondly, are there any other operations you can do to 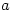 and
and 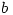 and the
and the 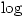 retains the same value? In other words:
retains the same value? In other words:
- Find all functions
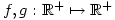 such that
such that 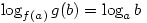 for all
for all 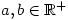
4 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
lhs = n \log_{a^n} b
= n \over \log_b a^n
=n / (n \times \log_b a )
= \log_a b
= rhs
Comment by msk — Tuesday 11 May 2004 6:44 pm #
Yes – that’s right. Another way to do it is to use the change of base formula to change the base of the LHS to a.
Can you solve the second problem?
Comment by steve — Tuesday 11 May 2004 6:58 pm #
Require that
(f(x))^n = f(x^n)
?
Comment by Ronald — Friday 11 March 2005 2:34 pm #
In fact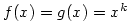 for some
for some 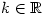
Comment by Steve — Friday 11 March 2005 3:08 pm #