Mathematics Weblog
Two Interesting Functions
Sunday 23 May 2004 at 10:33 am | In Articles | 2 CommentsAt A level students only see reasonably nice functions, though occasionally they come across
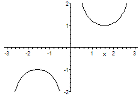
where the maximum is smaller than the minimum (which, incidentally, is why one should use the terms local maximum and local minimum instead).
But what they won’t have come across are functions like these:
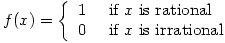
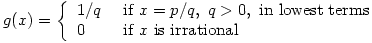
When trying to draw the graphs remember that
- between every pair of irrational numbers there is a rational number
- between every pair of rational numbers there is a irrational number
You can very roughly draw f using dots and there’s a nice picture of g at mathworld
Now think about integrating f and g – do they have areas under between them and the x-axis? The answer to ths question is important in the theory of integration.
These functions have other interesting properties and illustrate the relationship between rational and irrational numbers.
2 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Nice site. I love such functions.
Comment by Alex — Tuesday 25 May 2004 7:50 pm #
I just came across those functions f and g in Spivak’s “Calculus”. Trying to plot them both was actually quite fun and the result is interesting.
Comment by Tom — Sunday 24 October 2004 2:09 am #