Mathematics Weblog
This site uses LatexRender for the mathematics
Misunderstanding
Wednesday 16 June 2004 at 4:23 pm | In Articles | 1 CommentWhen teaching maths that you are familiar with, it is not easy to see why students struggle with it – indeed once the student has understood the problem, they can’t see why they had difficulty before! This means that you have to be very careful what you say in case an attentive student takes it literally.
How many times has a lecturer said “the integral of e is itself ” ? So this happens:
- Q. Find the value of
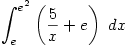
A. ![\displaystyle \int_e^{e^2}\left(\frac{5}{x}+e\right)\ dx=\left[5\ln |x| + e\right]_e^{e^2}=\dots=5 \displaystyle \int_e^{e^2}\left(\frac{5}{x}+e\right)\ dx=\left[5\ln |x| + e\right]_e^{e^2}=\dots=5](/maths/latexrender/pictures/e846d6c1a3346703ff51cd012cc2f2bb.gif)
When the error was pointed out to the student, they responded with
- Why does
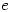 integrate to
integrate to 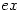 ?
? 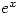 integrates to
integrates to 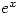 and as
and as 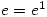 surely the integral of
surely the integral of 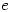 is also
is also 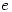 ?
?How would you respond to this?
1 Comment »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
oh, wow, that’s an interesting misconception.
ask the student to evaluate e as a decimal…
hopefully they will come up with the answer 2.718… and then they can see this is a constant.
Perhaps even starting with constant
k = 2.718 and getting student to integrate that would be a good way to go.
Comment by Ronald — Wednesday 22 December 2004 9:39 pm #