Mathematics Weblog
Powers
Friday 25 June 2004 at 3:37 pm | In Articles | 3 CommentsI was asked recently why 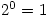 . Remember that if n is a positive whole number then
. Remember that if n is a positive whole number then 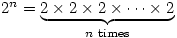 . Clearly you can’t multiply 2 by itself 0 times 😕
. Clearly you can’t multiply 2 by itself 0 times 😕
The key, when extending properties of the number system, is to use definitions that work for every number. So, for example
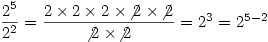
which gives you the rule that
- to divide powers you subtract the indices (the small superscripted numbers)
This leads to
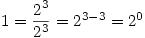
Similarly, 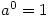 for any positive real number.
for any positive real number.
What about zero powers of non-negative powers? 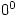 is a controversial case I have mentioned on 29 February (Q2.) and see Dr Math FAQ for more on this.
is a controversial case I have mentioned on 29 February (Q2.) and see Dr Math FAQ for more on this.
And if the number is negative? Great care is needed in this case. For example, using only real numbers, 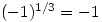 but
but 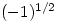 is not a real number. The problem arises because the general definition of a power is given by
is not a real number. The problem arises because the general definition of a power is given by 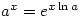 and
and 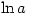 is undefined if a is negative or 0. Using complex numbers (which helps with
is undefined if a is negative or 0. Using complex numbers (which helps with 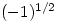 ) just makes things more complex 😕 – see Log of Complex Number
) just makes things more complex 😕 – see Log of Complex Number
3 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
I didn’t spot this article before… I would say that 1 is the multiplicative identity.
Or, in other words,
we know from laws of indices that:
2^0 * 2^n = 2^(0+n)
This goes for any base with the exception of 0
Even in the case of 0, I would be tempted to say that 0^0 is more 1 than anything else
Comment by Ronald — Wednesday 22 December 2004 11:42 pm #
missing superscripts… sorry
Comment by Ronald — Wednesday 22 December 2004 11:44 pm #
I have added them in for you 🙂
Comment by Steve — Wednesday 22 December 2004 11:48 pm #