Mathematics Weblog
This site uses LatexRender for the mathematics
Amazing Formula
Monday 11 October 2004 at 9:47 pm | In Articles | 3 CommentsThere are many interesting formulae in mathematics;
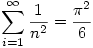
must be one of the most amazing of all.
The first reaction is where did that  come from? You can find 14 different proofs of this in a paper on Robin Chapman’s Home Page [look for Evaluating zeta(2)]
come from? You can find 14 different proofs of this in a paper on Robin Chapman’s Home Page [look for Evaluating zeta(2)]
Given this result can you prove another amazing result?
If you pick two positive integers at random, the probability of them having no common divisor is 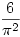
 gets everywhere! See Wikipedia for more such as
gets everywhere! See Wikipedia for more such as
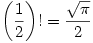 or
or 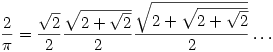 or
or 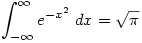
3 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
I don’t know if your probability makes sense…
How do you pick two positive integers at random?
Is it possible to pick at random from an infinite set?
Comment by Ronald — Sunday 14 November 2004 3:48 pm #
Have a look at http://www.physics.harvard.edu/probweek/sol44.pdf where they make the statement more precise:
To be precise about what we mean by probabilities in this problem, we really should
word the question as: Let N be a very large integer. Pick two random integers less
than or equal to N. What is the probability that these numbers are relatively prime,
in the limit where N goes to infinity?
Comment by Steve — Sunday 14 November 2004 4:10 pm #
That’s clever… thank you.
Comment by Ronald — Thursday 23 December 2004 12:18 pm #