Mathematics Weblog
I really despair
Saturday 4 December 2004 at 8:50 pm | In Articles | 4 CommentsI came across this answer, written over a year ago, to a question about division by zero. The answer was written by a Physics instructor who seems to be rather confused.
- Division by zero is often defined as infinity. Infinity divided by zero is infinity-squared. For signs to be defined correctly, you must have a +0 and a -0. This is often accomplished through the theory of limits. The limit of x as x approaches zero from the negative side is -0. The limit of x as x approached zero from the positive side is +0. Higer (sic) level mathematics uses the concept of infinity quite often.
Let’s gloss over the first two appalling sentences. In the following sentences I suppose he is trying to refer to the fact that one can approach 0 (or any number) from different directions. If x approaches 0 from above, that is x remains positive, then you can write, for example, 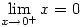 . Note that the limit is written as 0 not +0 which is of course equal to 0 so there’s no point writing it! This notation allows one to show that different things can happen if x approaches 0 from above or from below and to say that
. Note that the limit is written as 0 not +0 which is of course equal to 0 so there’s no point writing it! This notation allows one to show that different things can happen if x approaches 0 from above or from below and to say that 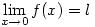 if and only if
if and only if 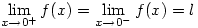 (where f is a real-valued function defined on a neighbourhood of 0).
(where f is a real-valued function defined on a neighbourhood of 0).
Personally, I like using 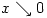 and
and  rather than
rather than 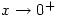 and
and 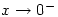 respectively, because they illustrate the approach from above or below.
respectively, because they illustrate the approach from above or below.
4 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Well if you despair with the physics prof then continue to despair because my math prof said he ain’t got no problem with saying 1/0 = infinity. He’s said it multiple times probably because he’s heard some people say they don’t believe that or whatever.
So can you give a good explanation of why you think its bogus instead of just complaining?
Heck my calculator even says 1/0 = infinity.
Comment by Red Rhubarb — Friday 10 December 2004 10:08 am #
You don’t have to believe me, try John Conway, a famous methematician at http://www.mathpath.org/concepts/division.by.zero.htm. As he says:
1/0 is the number c such that 0×c = 1. But there is no such number. So 1/0 has no meaning
There are 2 problems with saying :
: . So if
. So if  it would follow that 1=2 and similarly that all real numbers are equal! Division by zero is the hidden flaw in many paradoxes; see for example Classic Fallacies
it would follow that 1=2 and similarly that all real numbers are equal! Division by zero is the hidden flaw in many paradoxes; see for example Classic Fallacies doesn’t exist and
doesn’t exist and  is an idea not a number, what on earth does ‘=’ mean in
is an idea not a number, what on earth does ‘=’ mean in  ? Equals is an important symbol and should only be used with objects that are of the same type and have the same value, so has no meaning here.
? Equals is an important symbol and should only be used with objects that are of the same type and have the same value, so has no meaning here.
1. Division by zero is not allowed. It isn’t possible to define it without causing contradictions. For example,
2. Since
I have never come across a calculator that gives anything other than error when you divide 1 by 0. I asked my students today to check this and their calculators all give error as they should do.
Comment by Steve — Friday 10 December 2004 3:22 pm #
Intuitively, I’m with you on 1/0 != infinity. It has never made sense to me bacause I cannot find any x to satisfy x*0 = 1. My prof though did have an argument for why 1/0 = infinity is valid for him. He was using infinity as not a number but an idea that you could use any numbers a and b to make an algebraic relation related to 1/0 true, therefore, 1/0 is in a sense infinity. Sorry but I don’t remember the details of his argument.
As for what does “=” mean? Mathematicians and scientists are always pulling this kind of trickery. They define some doohickey not because it makes sense but because of convention (some guy a long time ago used it in the wrong way). How many times I’ve read someone complain that the notation is ambiguous or wrong!
As for the calculator thing, I don’t know what kind your students use but mine is a Hewlett Packard calculator.
I’m beginning to suspect that this division by zero thing is more of how you define your mathematics.
Comment by Red Rhubarb — Saturday 11 December 2004 6:35 am #
Re: your last comment…
THANK YOU!
I can never remember which way it means when someone writes
x -> 0+ or x -> 0-
Comment by Ronald — Wednesday 22 December 2004 7:43 pm #