Mathematics Weblog
Agnew’s Differential Equations
Sunday 5 December 2004 at 2:59 pm | In Articles | 3 CommentsWhen I studied differential equations, the set book was Ralph P Agnew’s Differential Equations. It had a brilliant index which seemed to contain every word in the book. Everything I ever wanted to look up was referenced in that index, unlike plenty of other textbooks.
It included a wonderful polemic about textbooks that claim that differential equations of order n have a general solution with n essential (aka arbitrary) constants:
- The promoted the view that to each differential equation of order n there corresponds an important family of solutions from which all other solutions … are obtainable by use of appropriate hocus-pocus involving envelopes and more complicated things. It was essential that this family of solutions should have a name (this is the start of the intimidation) which would immediately convince everybody that it existed and was important. With dubious regard for appropriateness of terminology, this family was called “the general solution” of the given equation.
He then says:
- It may be unclear whether this [differential equations of order n have n essential constants] is a theorem or a definition or merely a collection of words, but we are now in a realm where nearly everything is unclear. One thing, however, is clear. No meaning has been attached to the statement that a formula has n eseential constant. This gives the good old lecturer a chance to practice the art of proof by intimidation.
He then goes on to justify his remarks and includes as examples the differential equations 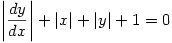 which has no solutions and
which has no solutions and 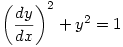 which has “vast hordes of real solutions“.
which has “vast hordes of real solutions“.
He also deals with the solution of 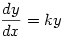 where dividing by
where dividing by 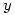 (the usual method taught at A level) won’t do since it could involve division by zero (the book indexes this as Division by zero taboo).
(the usual method taught at A level) won’t do since it could involve division by zero (the book indexes this as Division by zero taboo).
Finally, there is the wonderful snowplough problem (or snowplow as the author is American) which says:
- One day it started snowing at a heavy and steady rate. A snowplow started out at noon, going 2 miles the first hour and 1 mile the second hour. What time did it start snowing?
He says “Our first task is to recover from the shock of being asked to solve such a problem” and goes on “we assume that the plow clears snow at a constant rate of k cubic miles per hour“.
Now it’s up to you. Click on read more below for the time it started snowing.
It started snowing at around 11:23am. More precisely, 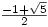 hours before midday.
hours before midday.
If you’re desperate the solution is in The Snowplow Problem by Ralph Agnew
3 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Er, “read more” doesn’t actually seem to go anywhere.
Comment by Anton Sherwood — Sunday 20 February 2005 7:40 pm #
‘read more’ works here in both IE & Firefox on Windows. Are you using something else?
Comment by Steve — Sunday 20 February 2005 7:59 pm #
If you can’t read it – this is what it says in ‘read more’: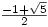 hours before midday.
hours before midday.
It started snowing at around 11:23am. More precisely,
If you’re desperate the solution is in The Snowplow Problem by Ralph Agnew
Comment by Steve — Sunday 20 February 2005 8:02 pm #