Mathematics Weblog

2 unrelated problems

Sunday 12 December 2004 at 2:26 pm | In Articles | 2 Comments

Using the Gelfond-Schneider theorem show that if 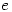is transcendental then $\pi$ is transcendental
If 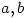are positive integers such that 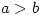and 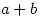is even, show that 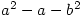is not a square

Notes

This theorem was being discussed at a seminar many years ago as was the transcendence of 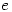. When we were told that it was an obvious consequence that $\pi$ is transcendental we thought that the speaker was joking. When he showed how it followed, there was a moment’s silence and then applause – one of those moments when one realises that mathematics is such a wonderful subject.
You can find an elementary proof (not using Gelfond-Schneider) of the transcendence of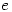 and $\pi$ here
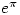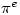It’s interesting to note that $e^{\pi}$ and $\pi^e$ are very close. In fact 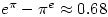$e^\pi-\pi^e \approx 0.68$ . See here
I came across this problem when looking through some old papers. I have no idea where it comes from (an old Mathematical Olympiad problem maybe??) or what the solution was.

Here’s a solution.
Suppose that x^2 = a^2 – a – b.
Then one finds that
4x^2 + 1 = (2a+2b-1)(2a-2b-1)
We are assuming that a & b have the
same parity, and that a>b are positive.
Thus 2a+2b-1 and 2a-2b-1 are both positive
integers of the form -1 mod 4. It’s easy to
see that such numbers have a prime factor
p of the form -1 mod 4. Thus 4x^2+1 has
a prime factor of the form p = -1 mod 4.
Now we are done, since all prime factors of
4x^2+1 are of the form 1 mod 4.
(This follows for example by quadratic
reciprocity).

Comment by Frank — Friday 18 February 2005 7:44 am #
Wonderful, thank you! Now why didn’t I see that 4x² + 1 = (2a+2b-1)(2a-2b-1)?

Comment by Steve — Friday 18 February 2005 2:21 pm #