Mathematics Weblog
This site uses LatexRender for the mathematics
Student Howlers
Saturday 18 December 2004 at 8:06 pm | In Articles | 4 CommentsA couple of howlers seen in sci.math newsgroup some years ago
1. I do like the lateral (?) thinking behind this one 😀
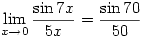
2. Problem
- Find
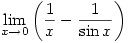
Answer
- Undefined
Proof:
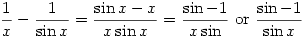
Therefore, since there are two possible answers with
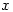 in the denominator and you can’t get rid of it and since
in the denominator and you can’t get rid of it and since 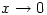 , the answer is undefined
, the answer is undefinedCancelling gives an example taken from Comic Sections by Desmond MacHale. Another one from the same book is:
3. Solve 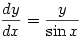
Solution:
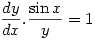 so
so 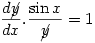 hence
hence 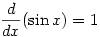 thus
thus 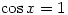 and
and 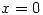
Do you have any favourite howlers?
4 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
I’ve found, through teaching, that a lot of kids stick with the misconception that
sin x
means
sin * x
for some mythical value ‘sin’.
It’s a nice way of making the brighter kids look like fools, I find! 😀
Comment by Ronald — Wednesday 22 December 2004 7:38 pm #
Yes I get that as well. I ask them if they use the button on the calculator when finding
button on the calculator when finding 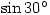 – it doesn’t help ❗
– it doesn’t help ❗
Comment by Steve — Wednesday 22 December 2004 8:06 pm #
In my classes, it most often occurs when I teach function notation. They have such a hard time grasping the fact that f(2) means the mapping f applied to 2 and all they have to do is substitute. So many of them substitute then multiply by 2 afterwards.
Comment by Scott — Monday 27 December 2004 8:10 am #
This is what an answer I got from a student – the question is “Do the product of two rationals equal a rational? explain.”
Answer:
It can be argued that two rational numbers cannot only produce rational
numbers because two signs such as + and – can when multiplied together
produce a negative which, in some cases, dooms the product to be
irrational. Besides, where to irrational numbers come from if not from
rationals? Is it not the rules that create the unruly? Even in the
definition of irrational we find rationality.
Hence, my argument is that two rationals can equal an irrational.
Comment by Desmond — Saturday 1 January 2005 12:24 pm #