Mathematics Weblog
Spherical Trigonometry
Saturday 8 January 2005 at 9:42 pm | In Articles | 8 CommentsThe idea that the angles of a triangle add up to 180° is so well engrained that it comes as a shock to some students that it isn’t true in other geometries. These geometries don’t have to be obscure or abstract since the angles of a spherical triangle drawn on the earth’s surface (assuming it is a sphere) always add up to more than 180° by an amount proportional to its area.
It’s a shame that like much else, spherical trigonometry has long since disappeared from the A level syllabus. The 2-dimensional sine rule
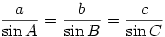
is (or ought to be 8-)) well-known but how many are aware of the 3-dimensional version
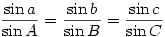
or the fact that the great circle distance (the shortest distance)  in nautical miles between points with latitude & longitude
in nautical miles between points with latitude & longitude 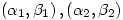 is given by
is given by
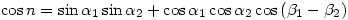
where  is measured in minutes? You could use sites such as Surface Distance Between Two Points of Latitude and Longitude but it’s not the same as sitting down and proving the general result.
is measured in minutes? You could use sites such as Surface Distance Between Two Points of Latitude and Longitude but it’s not the same as sitting down and proving the general result.
Without this introduction to three dimensions how is one going to start visualising geometry in four or more dimensions? Of course, reading Flatland would be an excellent start. Phoenix-Library has some excellent versions of this book in a number of online formats.
This is perhaps a suitable place to publicise my all time favourite puzzle:
- A hunter leaves his house one morning and walks one mile due south. He then walks one mile due west and shoots a bear, before walking a mile due north back to his house. What colour is the bear?
8 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
white? it’s a polar bear, seems easy after reading your post.
Comment by rv — Sunday 9 January 2005 10:24 am #
Yes, context is everything 🙂
But did you know that the walk is possible, not just at the North Pole, but at an infinite number of other places on the earth’s surface? The answer is still ‘white’ as there are no bears at these places.
Comment by Steve — Sunday 9 January 2005 11:23 am #
Where else is it possible? I can see it might be possible at the North Pole and at many, many places near the South Pole: for example, the hunter can trace over his steps as he walks the mile west.
Comment by Higherpi — Sunday 9 January 2005 12:30 pm #
By the way, thanks for this post. I didn’t realise spherical trig had ever been part of the A-level syllabus.
Comment by Higherpi — Sunday 9 January 2005 12:31 pm #
As far as I am aware, the journey is only possible near the poles, where the walk west is a complete (or multiple of a) circle of latitude. If you change the problem slightly so that the hunter starts walking south then you can allow him to cross the South Pole for yet more points.
I have a book (Trigonometry by C G Nobbs) written in 1962 for A level which covers spherical trigonometry. In those days there was much more variety in the various syllabuses. It is likely to have been in sixth form mathematics prior to A level. I do know that even subjects like projective geometry and inversion were in Scholarship Papers prior to their abolition in the mid-sixties (they were superseded by Special Papers).
Comment by Steve — Sunday 9 January 2005 12:56 pm #
True, the answer is white, but it’s interesting to point out the number of people who suggested it could be the south pole… There are no bears at the south pole nor anywhere in Antarctica for that matter.
Comment by Arima — Thursday 20 January 2005 1:07 am #
White; he must be at the north pole. This is actually not totally true from a geographical standpoint, but I won’t get into that!
Comment by MSM — Wednesday 13 April 2005 12:59 am #
I read your article re CG Nobbs and would love an email from you as I am related to him. He has in fact now died and I am on a mission to buy old books of his, thank you for your consideration.
Comment by Briget Granger — Saturday 9 September 2006 12:40 am #