Divisors

Sunday 30 January 2005 at 8:25 pm | In Articles | 2 Comments

Most people, when asked how many divisors the number 60 has (including 1 and 60), would struggle to do so without listing them all. Yet once you know that the prime factorisation of 60 is 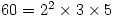60=2^2\times3\times5 you can immediately say that the number of divisors is 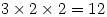3 \times 2 \times 2=12. In other words, you take each index, add 1 then multiply them together.

This is easy to see if you list the divisors as

    \2^0\times3^0\times5^0\ 2^1\times3^0\times5^0\ 2^2\times3^0\times5^0\ 2^0\times3^1\times5^0\ 2^1\times3^1\times5^0\ \cdots\ 2^2\times3^1\times5^1\

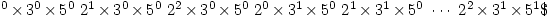
It’s then not difficult to prove the general result:

    If 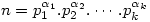n=p_1^{\alpha_1}.p_2^{\alpha_2}.\cdots.p_k^{\alpha_k} then the number of divisors of n is d(n)=\prod\limits^k_{i=1}\left(\alpha_i + 1}\right)

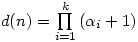
2 Comments »

RSS feed for comments on this post. TrackBack URI

  1. I really like this result.
    You can use it to show that the numbers with an odd number of factors must be square.

    Comment by Ronald — Sunday 30 January 2005 10:13 pm #

  2. I saw something like this while preparing for a math contest. It’s an interesting little result–I used something very similar to it to find the number of perfect square divisors of a given number.

    Comment by Anna — Wednesday 2 February 2005 10:19 pm #

Leave a comment

XHTML: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^