Mathematics Weblog
This site uses LatexRender for the mathematics
Simple?? Problem
Sunday 22 May 2005 at 7:13 pm | In Articles | 4 CommentsCan you prove that:
- if you have
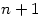 integers less than or equal to
integers less than or equal to 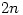 then there are always two of them which are relatively prime?
then there are always two of them which are relatively prime?This problem comes from the biography of Paul Erdös, The Man Who Loved Only Numbers. Erdös posed this problem to Louis Pósa, who was 12 at the time and a child prodigy, and who solved it in about 10 minutes.
This is one of those problems where you can spend hours getting nowhere, and yet the proof is actually very simple 😕
4 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
I believe that Pósa answered it in much less than ten minutes:
“Actually I discovered this simple result some years ago but it took me about ten minutes to find the really simple proof. Pósa sat there eating his soup and then after half a minute or so he said ‘If you have n+1 positive intergers less than or equal to 2n, some two of them will have to be consecutive and thus relatively prime.'”
Interesting article. 🙂
Comment by Tom — Sunday 22 May 2005 8:58 pm #
My version of the book doesn’t mention ‘after half a minute’. But you’re right though – Erdös had taken 10 minutes to solve it while Pósa solved it while eating his soup.
Comment by Steve — Sunday 22 May 2005 9:48 pm #
In fact, according to “Proofs from the BOOK” (an excellent book, by the way), the problem which Pósa solved while eating his soup is: given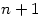 integers from
integers from  , prove that there is always one which divides another. This problem is similar but a little trickier.
, prove that there is always one which divides another. This problem is similar but a little trickier.
Comment by Cosmin — Monday 23 May 2005 11:14 am #
pigeonhole principle
Comment by guest — Wednesday 13 July 2005 9:23 am #