Mathematics Weblog
Summer Reading
Monday 11 July 2005 at 5:25 pm | In Articles | 7 CommentsI finally succumbed and bought Martin Gardner’s Mathematical Games: The Entire Collection of His Scientific American Columns. Of course, as it had to be sent from America, the postage wasn’t cheap and it locked up my computer when I first tried it. Turning off CD autorun solved that problem.
Now I can spend the summer reading all those articles I’ve never read or even only half-remembered. The ability to search all the articles is a real boon. Did you know, for example, pi is mentioned 5645 times in the books?
In Fractal Music, Hypercards and More… Martin Gardner refers to the 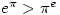 problem (which I’ve mentioned before) and says:
problem (which I’ve mentioned before) and says:
- Dozens of proofs have already been published. One of the shortest is based on the fact from elementary calculus that
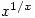 has a maximum value when
has a maximum value when 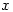 equals
equals 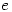 . Hence
. Hence 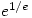 is greater than
is greater than 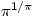 . Multiplying each exponent by
. Multiplying each exponent by 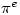 and canceling yields the inequality
and canceling yields the inequality 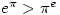 .
.The perils of publishing mathematics 😕 Can you spot the error and correct it?
7 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Multiplying exponents does not maintain the inequality as it means that you are multiplying each side by different amounts?
Comment by rohit khetan — Wednesday 13 July 2005 2:21 pm #
You can multiply exponents as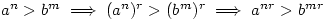 which means that you have multiplied the exponents by
which means that you have multiplied the exponents by 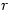 .
.
But you are in the right area – think about what you are multiplying by.
Comment by Steve — Wednesday 13 July 2005 3:17 pm #
multiply exponents by pi*e rather than pi to the power e.
Comment by rohit khetan — Friday 15 July 2005 6:04 am #
rohit’s right. i guess the formal(?) way to say it would be to exponentiate both sides by e*pi, right?
Comment by BL — Friday 15 July 2005 6:09 am #
You got it. I expect somewhere in the publishing process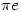 got transposed to
got transposed to 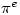 . The problem with typing mathematics that such errors, which are easy to make, can invalidate the result.
. The problem with typing mathematics that such errors, which are easy to make, can invalidate the result.
Comment by Steve — Friday 15 July 2005 10:31 am #
Yes, but you actually multiply the larger side by a larger amount.
Comment by guest — Friday 29 July 2005 7:23 am #
I think it best to think of it as raising both sides to the same power. You can say the sides are being multiplied by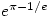 and by
and by 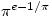 but how do you know one is larger than the other without assuming what you are trying to prove?
but how do you know one is larger than the other without assuming what you are trying to prove?
Comment by Steve — Friday 29 July 2005 10:18 am #