Odd one out

Wednesday 3 August 2005 at 6:38 pm | In Articles | 5 Comments

You may well have seen those questions which ask “Which is the odd one out?”, and you often get them as part of a so-called intelligence test 😮
What the question really says is “Which one does the questioner think is the odd one out?”. So it becomes a rather more difficult test of trying to read someone else’s mind and nothing to do with your ability to solve a problem.

Here’s an example of a mathematical “odd one out” to show what I mean. Here are 4 ‘true ‘ statements:

    a.  1 + 1 = 0          true in 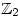\mathbb{Z}_2, arithmetic modulo 2
    b.  1 + 1 = 2          true in 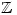\mathbb{Z}, ring of integers
    c.  1 + 1 = 10         true in binary
    d.  1 + 1 = 11         true for string concatenation in Basic

The odd one out could be

    b.  because it is the only one that is true in \mathbb{Z}
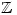
    d.  because it is the only one that doesn’t involve addition
    a.  because it is the only one where the right-hand side is less than 1 (using ordering in \mathbb{Z})
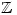    c.  because it is the only one where I can’t think of a reason (self-contradictory of course!)

Next time you come across one of those problems, see if you can give a reason why every one of the possibilities could be the odd one out.

5 Comments »

RSS feed for comments on this post. TrackBack URI

  1. I saw something similar to this recently (can’t remember where) in which the person said that IQ tests asking people to give the next number in a sequence are not a test of intelligence, since a search on the Online Encyclopedia of Integer Sequences can match up say 2, 4, 6, … with tonnes of sequences, many which won’t have 8 as the next term! So say you spot the pattern as something to do with the Riemann Zeta Function and claim the next number is 1223 (I’m making this up for the sake of argument), does that make you dumber than the average person who’d say 8?

    Comment by Craig — Thursday 4 August 2005 3:01 pm #

  2. I do so agree with that. I usually demonstrate this by using the sequence 1,2,4,8,16,31 which is the maximal number of regions obtained by joining n points around a circle by straight lines and is given by the formula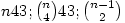 n + \binom{n}{4} + \binom{n-1}{2} Online Encyclopedia of Integer Sequences A000127

    I see from there that this sequence is also the number of regions in 4-space formed by n-1 hyperplanes, but I daren’t say that, otherwise I end up arguing with people who insist that time is the 4th dimension

    Comment by Steve — Thursday 4 August 2005 3:44 pm #

  3. a reason for answer c is:

    true only in integer bases b

    Comment by Polymath — Sunday 21 August 2005 7:53 pm #

  4. sorry, that last comment should read:

    true only in integer bases b where b is less than 3.

    Comment by Polymath — Sunday 21 August 2005 7:54 pm #

  5. Well, c would be for instance because it’s the only one truly dependent on a chosen base to represent it in instead of more “ephemeral” qualities of the value.

    Comment by Michi — Monday 20 February 2006 12:10 pm #

Leave a comment

XHTML: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^