Mathematics Weblog
Function Notation
Sunday 25 September 2005 at 6:17 pm | In Articles | 9 CommentsThe notation 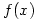 is very common and is taught at A level (and sometimes earlier) in the UK. It’s well understood and used but has one well-known flaw – composition of functions.
is very common and is taught at A level (and sometimes earlier) in the UK. It’s well understood and used but has one well-known flaw – composition of functions. 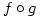 or just
or just 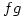 is defined by
is defined by 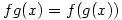 . The problem here is that
. The problem here is that 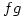 means do g first then f, rather than the other way round and is therefore counter-intuitive to the beginner.
means do g first then f, rather than the other way round and is therefore counter-intuitive to the beginner.
One solution is to use a different notation for functions and use 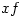 instead of
instead of 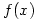 . It’s certainly more economical to write but, more importantly, the composite function
. It’s certainly more economical to write but, more importantly, the composite function 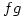 is defined by
is defined by 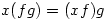 , which means do f then g. This seems to be much nicer if it weren’t for one thing. As far as I know, this notation is only taught in advanced courses (3rd year degree/postgraduate) and in books like Universal Algebra by P M Cohn, which is certainly not meant to be read by a novice. By this time, the
, which means do f then g. This seems to be much nicer if it weren’t for one thing. As far as I know, this notation is only taught in advanced courses (3rd year degree/postgraduate) and in books like Universal Algebra by P M Cohn, which is certainly not meant to be read by a novice. By this time, the 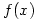 is so engrained in a student’s mind it is quite difficult to change to
is so engrained in a student’s mind it is quite difficult to change to 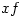 – it certainly was for me 😕
– it certainly was for me 😕
Does anyone know if the 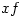 notation is taught in more elementary mathematics courses; if so, how was it received?
notation is taught in more elementary mathematics courses; if so, how was it received?
9 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
Would you then advocate writing (x)sin instead of sin(x)?
Comment by Andy — Monday 26 September 2005 5:45 am #
Good point, although on older pre-VPAM calculators that is exactly what one had to type
Comment by Steve — Monday 26 September 2005 12:21 pm #
I’ve taught high school math in the U. S. for almost 20 years, and in the Int’l Baccalaureate for about half that time. I’ve never run into the notation xf notation at this level (although it doesn’t look completely foreign to me, so I probably saw it in my youth).
IB uses “f : x ↦” rather than “f(x) =” The thing I like about this is that it keeps kids from thinking that the function rule is an equation that needs solving rather than a statement of the operation that the function does.
(I tried to insert an arrow with unicode; it’s decimal 8615 or hex 21A6.)
Comment by Peggy — Monday 26 September 2005 9:50 pm #
I think you meant 8614 (=21A6) so I’ve changed it. IE can’t show it but it looks fine in Firefox.
For those using IE, Peggy is saying: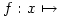 ” rather than “
” rather than “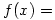 ”
”
IB uses “
Comment by Steve — Monday 26 September 2005 10:15 pm #
Hm, when I was in college (in the US), I was taught that f composition g means do f, and then g, and so when you write it in composition notation it is in a different order than when you write it out fully, say g(f(x)). So I always thought that this was the standard, until I went to grad school and it was done the “normal” way.
But I have never seen “xf” before, not in high school, college or graduate school.
Comment by wing — Saturday 8 October 2005 2:06 am #
Just fyi, this notation is employed by Herstein in his book “Topics in Algebra” which is perhaps as elementary an introduction to abstract algebra as any.
Comment by bhargav — Thursday 13 October 2005 12:11 pm #
Ooh yes, so it does! Fascinating!
Comment by Steve — Thursday 13 October 2005 8:38 pm #
In the French Baccalaureate:
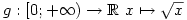
Functions are introduced in the IB style here in “Premiere” (Year 12 in the UK, AS level).
For example
the function g is defined as such:
http://perso.wanadoo.fr/gilles.costantini/Lycee_fichiers/CoursP_fichiers/genefct.pdf this might be of help.
I very much doubt the IB never uses the g(x) way. In the latter part of the FB course, g(x) is always used
For composite functions, I don’t see what’s the big deal? You just work from right to left. If students are explained well, and warned of the dangers in the lesson I think there are no problems with it at all.
For composite functions this would be the FB of doing things:
http://perso.wanadoo.fr/gilles.costantini/Lycee_fichiers/CoursP_fichiers/compfct.pdf
Comment by Luc — Friday 31 March 2006 5:31 pm #
I find it hard to understand examples such as fg(x) if f= x3 and g= 1/x-2.
Comment by Martina — Thursday 12 February 2009 6:04 pm #