Mathematics Weblog
Cubics
Thursday 26 January 2006 at 9:26 pm | In Articles | 1 CommentA problem that I give some of the students is to show that for a cubic 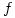 that if
that if 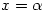 and
and 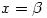 are the x-coordinates of its stationary points then
are the x-coordinates of its stationary points then 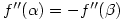 . Hopefully, they will have already noticed this result in the exercises they have done.
. Hopefully, they will have already noticed this result in the exercises they have done.
I then ask them to show that the point of inflexion of 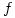 is at the midpoint of the turning points. This involves using the equations for the roots of a quadratic:
is at the midpoint of the turning points. This involves using the equations for the roots of a quadratic: 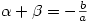 and
and 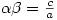 but the algebra isn’t particularly nice (details are here).
but the algebra isn’t particularly nice (details are here).
It dawned on me that there’s a better way which is not only simpler to prove but gives a more powerful result: a cubic is (rotationally) symmetric about its point of inflexion.
To see this, take the cubic and translate it so that the point of inflexion is at the origin. This clearly has no effect on the symmetry so it is sufficient to prove the result in this case.
If 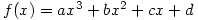 has its point of inflexion at the origin then clearly
has its point of inflexion at the origin then clearly 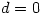 and, as
and, as 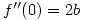 , it follows that
, it follows that 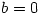 so
so 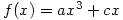 . Rotate this by
. Rotate this by  about the origin, for example by applying the usual matrix
about the origin, for example by applying the usual matrix 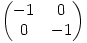 , and you get
, and you get 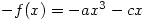 which is clearly the same cubic. Hence it has rotational symmetry about the origin, and in particular, the point of inflexion at the origin is the midpoint of the stationary points.
which is clearly the same cubic. Hence it has rotational symmetry about the origin, and in particular, the point of inflexion at the origin is the midpoint of the stationary points.
Some textbooks misuse infinity
Monday 18 October 2004 at 3:43 pm | In Articles | Post CommentIt’s happened again!  used in a textbook (unnamed to protect the guilty) as if it were a real number instead of an idea. In a discussion of the formula for the acute angle
used in a textbook (unnamed to protect the guilty) as if it were a real number instead of an idea. In a discussion of the formula for the acute angle 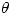 between two lines
between two lines
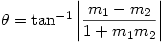
the following appears:
- Putting
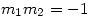 gives an angle
gives an angle 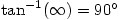 , confirming the condition for the lines to be perpendicular
, confirming the condition for the lines to be perpendicular This is of course complete nonsense. As I’ve said before 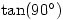 doesn’t exist and
doesn’t exist and 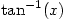 is only defined on
is only defined on 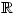 ie for
ie for 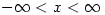
The textbook was written by the examiners (which is one reason why we use it); this worries me even more.
I suppose this is better than one well-known textbook back in the eighties which solved the equation 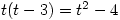 by putting
by putting 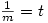 then ‘showing’
then ‘showing’  or
or 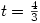 . This seems to show that all linear equations are quadratics in disguise; or cubics, quartics – who knows where this nonsense leads 😕
. This seems to show that all linear equations are quadratics in disguise; or cubics, quartics – who knows where this nonsense leads 😕
See also Division by zero shock!
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^