Mathematics Weblog
Don’t Miss This!
Saturday 28 October 2006 at 6:26 pm | In Articles | Post CommentFrom Mathematics Under The Microscope:
- On Thursday, 2 November, in the programme In Our Time on BBC Radio 4 (9.00-9.45am, repeated 9.30pm), Melvyn Bragg and guests will discuss Poincare Conjecture.
It will also be available on Listen Again for a further week after the broadcast.
Mathematics is hard
Tuesday 24 October 2006 at 10:43 am | In Articles | 3 CommentsA number of blogs have picked up on a US report that says:
- that countries with students who say they enjoy mathematics scored much lower than countries that rank lower in mathematics enjoyment
The nations with the best scores have the least happy, least confident math students
We might want to focus on the math that kids are learning and just be a little less obsessed with the fact that they have to enjoy every minute of it
Other countries do better than the United States because they seem to expect more from students. That could also explain why high performers in other nations express less confidence and enjoyment in math. They consider their peer group to be star achievers.
Even efforts to make math relevant may be irrelevant, says the study
Nations that try to teach math in terms of daily life have the lowest test scores.
(the full report is available here)
These ideas may seem astonishing, yet to many battle-scarred maths teachers it is what they have been saying for years. Mathematics is hard and it requires dedication, effort and time to understand it. This is not popular so in the UK we have decided to get round the problem by making the subject easier, delivering it in small easily-digestible lumps and as formulaic as possible so anyone can follow it. To prove we are delivering (ha!) we test and re-test making sure that the questions we set are virtually identical each year and again, divide up into little pieces.
It’s a bit like teaching someone to ride a bike by ensuring that they always use stabilisers. Learning to maintain balance takes lots of time and practice and the same is true of mathematics. Yet in the end we lose out. The cyclists never discover the excitement and freedom of cycling alone and the mathematics student never discovers the beauty of mathematics, forever imprisoned by having to apply the same tedious but not understood methods to the same problems.
Ian Stewart in Concepts of Modern Mathematics puts it this way:
- the technical grind is not just an afterthought: it is an absolutely essential part of the process … The problem with the hard technical grind is that there is no way to appreciate it except by doing it … If we can get away from the alarming habit that has grown up of shying away from anything that is the least bit difficult, then we may make real progress.
Mathematics is hard and we do ourselves a disservice by denying or avoiding it. More, not less, time should be devoted to it in schools and colleges so that students have time to practice and have the opportunity to really think; only then will come understanding.
You can (and should) read more about this topic at
Mathematics Under the Microscope
NeverEndingBooks (from Belgium, top western country for mathematics according to a survey on which the report is based)
The Reference Frame
You may wish to contribute to this discussion on Gooseania’s blog.
PS Today’s Education Guardian has an article Four steps to being chucked on the scrapheap which describes the problems that arise with the formulaic approach to teaching any subject. The author, an experienced teacher, writes very well. I have always said that OFSTED inspired teaching plans are bollocks but now I can put it so much better and say
- a lesson plan goes together with good teaching like a horse and gherkin
Stretching Question 2
Friday 13 October 2006 at 3:14 pm | In Articles | 3 CommentsIn Stretching Question I wondered how students would cope with a type of question they wouldn’t have seen before:
- If
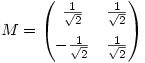 calculate
calculate 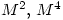 and
and 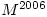
The examiners’ report is now out and it says (edited to show context)
- Attempts at calculating
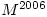 were rarely completely successful. Many candidates found that
were rarely completely successful. Many candidates found that 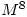 was the identity matrix but then went on to say that
was the identity matrix but then went on to say that 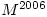 must also be the identity matrix. Others gave the value of
must also be the identity matrix. Others gave the value of 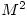 or gave the correct answer without any indication as to their reason for doing so, or with incomplete reasoning.
or gave the correct answer without any indication as to their reason for doing so, or with incomplete reasoning.How disappointing that so few managed to complete the question successfully. The lack of reasoning doesn’t tell us whether students guessed or found it too easy to bother putting down the working. It might have helped if students were taught that if 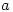 and
and 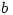 are integers then there exist integers
are integers then there exist integers 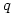 and
and 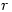 with
with 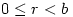 such that
such that 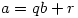 but these fundamental ideas seemed to have been lost to A level.
In the first AS exam the examiners comment that
but these fundamental ideas seemed to have been lost to A level.
In the first AS exam the examiners comment that
- When asked to use the Factor Theorem or Remainder Theorem, no marks can be earned for using long division.
which means
- British students haven’t a clue how to do long division of polynomials so we’ve made it easier for you, so don’t try and pretend you know best. (See A Level Exam Questions).
Blackboards
Tuesday 10 October 2006 at 1:45 pm | In Articles | Post CommentPress coverage has led me to Psychophysiology of Blackboard Teaching, Revisited which of course refers to the original article written in August. My only disappointment is that it is now too late to add anything useful to that article.
My experience in working in a College and for the Open University is that very few people understand anything about the teaching of mathematics. They seem to think that a few square centimetres of white board is sufficient and, nowadays, it can all be done ‘using a computer’ though those that say this can barely find the on-switch of a computer.
I have had battles in the past to get decent writing surfaces. I am happy with blackboards or whiteboards providing they provide very large surfaces. In fact they would have to be roller boards in order to accommodate the area I need. Even when you get what you want, few people think about maintenance so you end up with boards that are in a disgusting state and impossible to use. It helps if the previous user would clean the board after they have finished.
I don’t object to people being ignorant about how mathematics should be taught; what really gets me is their arrogance that they know best.
So good luck to Alexandre Borovik’s campaign! Do read Psychophysiology of Blackboard Teaching about the importance of blackboards in mathematics teaching.
Alternative Arithmetic
Sunday 8 October 2006 at 1:01 pm | In Articles | 1 Comment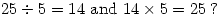 See Maths Lesson in the Mathematics Under the Microscope blog for a ‘proof’.
See Maths Lesson in the Mathematics Under the Microscope blog for a ‘proof’.
The film clip is amusing but just pause to think how much damage is done by non-specialist mathematics teaching. Good maths teachers should be nurtured and valued but they certainly aren’t in the UK. Grrr!
iPod Shuffle and Randomness
Saturday 7 October 2006 at 1:20 pm | In Articles | 1 CommentIn an article Oh no, not Steely Dan again published in todays’ Guardian colour magazine, Steven Levy explains, in layman’s terms, why the iPod’s shuffle produces seemingly non-random results (so Steely Dan appears to be played more than other artists on his iPod) yet Apple’s engineers reassure him that the code does produce randomness.
The article has a lovely quote:
- “Our brains aren’t wired to understand randomness – there’s even a huge industry that takes advantage of people’s inability to deal with random distributions. It’s called gambling.”
The way Apple dealt with this apparent non-randomness is fascinating.
The article quotes Brian Hansen’s experiments which you will find at How Much Does iTunes Like My Five-Star Songs?.
Back in the 1970s the Open University’s first level course M100 discussed the problem of defining randomness. It was usually defined in terms of probability which was itself defined in terms of randomness but it didn’t discuss Claude Shannon’s important contribution mentioned in the article. You can read more about randomness at Wikipedia.
This article (an edited extract from a forthcoming book about the iPod The Perfect Thing) should be required reading for everyone.
No it doesn’t need a maths degree!
Wednesday 4 October 2006 at 1:58 pm | In Articles | 1 CommentThis sort of thing rather winds me up. In an article titled “Energy switch needs a maths degree” the Guardian consumer column tries to make out that energy bills are impossible to check. It then, in a very objectionable manner, tells you how to do so. All it involves is simple arithmetic, which I would hope any GCSE student would be capable of. Why does the Guardian have to keep promoting the idea that arithmetic that uses a calculator is far too difficult for anyone without a maths degree? Perhaps they need maths teaching because they get the calculation wrong!
Here is an edited version of the article:
- …you need a degree in mathematics to be able to compare the different providers accurately…
Those who have not yet lost consciousness and are eager to make their own calculations read on (this is not for the faint-hearted). Subtract the previous meter reading from the present figure. If you have an imperial meter (normally four digits) then multiply the figure by 2.83 to convert to metric. Multiply the result by 1.02264 to work out the temperature and pressure volume correction (don’t ask!). The bill will show a calorific value figure so multiply your figure by this number and if your maths is any good you should be left with 39 or 40. Divide by 3.6 to calculate how many units have been used, then multiply the units by the tariff price.
Add standing charge if applicable and 5% VAT, stir well and bake at gas mark 6. Alternatively, pour a gin and do something more interesting with your life.
What is it about our culture that so denigrates mathematics?
Here is the email I wrote to the Guardian’s consumer column. We’ll see if they take any notice.
Princeton Maths Competition
Wednesday 4 October 2006 at 1:09 pm | In Articles | Post CommentI wouldn’t normally do this, but it is always good to encourage young mathematicians so I am reproducing this email to help publicise this appeal.
Hello,
I am an avid reader of your blog, and I thought that perhaps you could help us. I am proud to announce the formation of Team Carolina, a group of students who will be competing at the Princeton Math Competition this December. This group of unusually bright students includes former IMO gold medalist Arnav Tripathy, one of the top 6 high school mathematicians in the USA, and one of only 41 IMO gold medalists in the world. Because of the unusually talented team we have put together this year, we are excited about Team Carolina’s chance to win the competition this year, and bring academic glory to the Carolinas. But we need your help. The cost of the trip is quite expensive, around $3500, and we cannot do it without sponsors. We thus ask that you donate any amount you can to help us make the trip to Princeton.
You can donate online, and all donations are tax-deductible. Any donations over $500 will result in the Princeton Math Club itself giving you official sponsor status, but again, every little bit helps. You can donate online through the Art of Problem Solving Foundation by clicking here. (The Art of Problem Solving Foundation is a 501(c)3 charitable organization). Under the “Designation” field, please put “Princeton Math Club – Team Carolina”. If you decide to donate, please email me as well, and we will include you on our t-shirts. This is an excellent way to promote your business or honor a loved one. All donations are tax-deductible, as described on the website. Thank you so much for any help you can give us. If you have any questions, please feel free to email me, or the coordinator of the Princeton Math Competition, Nathan Savir. nsavir@princeton.edu
Sincerely,
Sean Soni
Team Carolina 2006
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^