Mathematics Weblog

Dumbing Down

Thursday 29 March 2007 at 12:47 pm | In Articles | 4 Comments

There’s a fascinating post at The Unapologetic Mathematician called Math and science testing in public schools which says that, because many students are failing the current maths and science tests, Washington state is proposing that they should be replaced by easier end of course tests:

I went to public schools in Maryland, where we had similar exams. Those students sharing my cynical bent referred to them as the “functional idiot tests”. I really do mean that it mostly tested respiratory function. I passed two of them by filling in pseudorandom bubbles and never actually opening the test booklet.

This picture of dumbing down will be familiar to British readers. This quote from the same post

This is exactly what Washington state is about to do. The important thing is evidently not to teach mathematics or science to its students. It’s to draw the target after we know where they land — give them a test we know they can pass.

echoes some of the controversy over new GCSE Science exams to be taken by 16 year olds Critics attack new science GCSE. I have never met any mathematics teacher who isn’t convinced that mathematics in the UK has been dumbed down quite considerably. The one attempt in 2000 to redress this problem ended in miserable failure and so the slide downwards has continued.

But there’s another issue here. In Britain, over at least the last 100 years or more, there has been an attempt to democratise education in the sense that, where only elites stayed on at school beyond the age of 14 in the early 20th century, there are proposals to raise the school leaving age to 18 and ensure that 50% of the population go on to higher education. It means that studying mathematics is compulsory at least until the age of 16.

This is good but the effect has been to simplify the syllabus substantially to allow more students to succeed. Examination questions set in the early twentieth century on complicated algebraic manipulation or a question on inversion (see * below) set in 1962 could not be set now. So the question that needs to be asked is

Is it possible to teach mathematics to a larger range of students without compromising on the level taught?

Alexandre Borovik’s book Mathematics under the Microscope in the section 4.6 Mental arithmetic and the method of Radzivilovsky details a radical approach by “a brilliant and idiosyncratic mathematics teacher, Vladimir Radzivilovsky” who

systematically builds bridges between various mental presentations of order and number in his pupils’ heads

and

Radzivilovsky’s success is measured by the fact that, among his former students, he can name dozens of professional mathematicians, physicists and computer scientists

There must be others who have ideas about teaching mathematics to a wide range of students whilst still maintaining standards.

* Here is an inversion question taken from a University of London A level Paper III Summer 1962:

Prove that the inverse of the point with respect to the circle is

Find the equations of the inverses of the circles

and

with respect to the circle .

Deduce that and intersect at right angles.

How To Write Mathematics Badly 3

Friday 16 March 2007 at 4:44 pm | In Articles | 8 Comments

Most of the advice on writing mathematics in the previous posts is aimed at the postgraduate student or those writing papers. Yet many of us are all too keenly aware that undergraduate students are in even greater need of help. For example,

• misuse of the equals sign; I’ve lost count of the number of times have I told students that both sides of = must be of the same type so a function doesn’t equal a point in 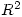and ‘equals’ is not a synonym of ‘therefore’ or ‘implies’;
• sentences that are missing one or more of subject, verb, object;
• steps in a proof that have no relation to what has gone before;
• etc …

I am pleased to say that Dr Kevin Houston of Leeds University has written to me to tell me how he is trying to help students to write properly:

I am writing a book called How to Think Like a Mathematician which includes a bit about writing mathematics at university (but can be applied at lower levels). This is aimed at first degree students – I notice that a lot of advice about writing maths is aimed at PhD students, for example, the video of Serre.

The sample chapter on writing is on my website along with the full booklet that we give to our first year maths students here at Leeds.

A couple of quotes taken at random:

An equation involves saying that two expressions are equal, for example, 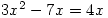. Note that an inequality, such as 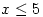, is not an equation.

‘The number of people over 40 = 5’, which reads all right, but the eye is drawn to the (erroneous) expression 40 = 5.

Well-worth reading!