Mathematics Weblog
Dumbing Down
Thursday 29 March 2007 at 12:47 pm | In Articles | 4 CommentsThere’s a fascinating post at The Unapologetic Mathematician called Math and science testing in public schools which says that, because many students are failing the current maths and science tests, Washington state is proposing that they should be replaced by easier end of course tests:
I went to public schools in Maryland, where we had similar exams. Those students sharing my cynical bent referred to them as the “functional idiot testsâ€. I really do mean that it mostly tested respiratory function. I passed two of them by filling in pseudorandom bubbles and never actually opening the test booklet.
This picture of dumbing down will be familiar to British readers. This quote from the same post
This is exactly what Washington state is about to do. The important thing is evidently not to teach mathematics or science to its students. It’s to draw the target after we know where they land — give them a test we know they can pass.
echoes some of the controversy over new GCSE Science exams to be taken by 16 year olds Critics attack new science GCSE. I have never met any mathematics teacher who isn’t convinced that mathematics in the UK has been dumbed down quite considerably. The one attempt in 2000 to redress this problem ended in miserable failure and so the slide downwards has continued.
But there’s another issue here. In Britain, over at least the last 100 years or more, there has been an attempt to democratise education in the sense that, where only elites stayed on at school beyond the age of 14 in the early 20th century, there are proposals to raise the school leaving age to 18 and ensure that 50% of the population go on to higher education. It means that studying mathematics is compulsory at least until the age of 16.
This is good but the effect has been to simplify the syllabus substantially to allow more students to succeed. Examination questions set in the early twentieth century on complicated algebraic manipulation or a question on inversion (see * below) set in 1962 could not be set now. So the question that needs to be asked is
Is it possible to teach mathematics to a larger range of students without compromising on the level taught?
Alexandre Borovik’s book Mathematics under the Microscope in the section 4.6 Mental arithmetic and the method of Radzivilovsky details a radical approach by “a brilliant and idiosyncratic mathematics teacher, Vladimir Radzivilovsky” who
systematically builds bridges between various mental presentations of order and number in his pupils’ heads
and
Radzivilovsky’s success is measured by the fact that, among his former students, he can name dozens of professional mathematicians, physicists and computer scientists
There must be others who have ideas about teaching mathematics to a wide range of students whilst still maintaining standards.
* Here is an inversion question taken from a University of London A level Paper III Summer 1962:
Prove that the inverse of the point
with respect to the circle
is
Find the equations of the inverses of the circles
and
with respect to the circle
.
Deduce that
and
intersect at right angles.
4 Comments
Sorry, the comment form is closed at this time.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
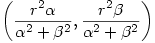
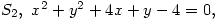
I think it’d be interesting to see how many people actually went on to do maths in 1962. I’d previously never heard of the concept ‘inversion’ in maths!
To answer the question, it is possible in my opinion, but it’s not a simple matter! That’s why I’m wondering what it used to be like in 1962. If it worked then, there’s really no reason why it shouldn’t work now.
Or maybe do you think that they should have seperate qualifactions for people at different levels? I don’t really know what I’m saying here, but I’m currently reading ‘Letters to….’ and Ian Stewart commented that his school maths teacher used to give him and a few friends extra lessons, i.e. pushing them further. So in their normal lessons the teacher didn’t teach them maths, but the rest of the class. Is this divide necessary? Well it gives the able students a bigger challenge, and ultimately prepares them better, whilst the ‘less able’ ones don’t lose out.
[oops sorry for long reply! It’s probably because I’m not posting one on my own blog today 😮 ]
Comment by beans — Thursday 29 March 2007 7:33 pm #
Inversion is behind the non-Euclidean universes of the artist M.C. Escher whose works so appeal to mathematicians. See for example the Circle Limit picture in the Hyperbolic Geometry section of Mathematical mysteries: Strange Geometries. The universe can be thought of one in which, to the outside observer, lengths shrink as one gets nearer the edge of the disk. Thus it is an example of an infinite but bounded universe.
Comment by Steve — Thursday 29 March 2007 10:17 pm #
Hi, i was googling for math-related blogs to promote my fresh-out opensource graphical calculator. To me it is still a really useful and fun mathtoy and increases intuitive feel for functional behavouir. I wrote an article on it here: http://www.rikarends.com/riks-calculator
As i couldn’t find an email address i decided to post a comment. I’m just trying to get word out a bit, as else nobody will ever find the fruits of my labour :). I’m also curious about the responses on it from more serious math-heads.
Regards,
Rik Arends
Comment by Rik Arends — Wednesday 11 April 2007 1:26 pm #
[…] Dumbing Down I mentioned the concern about mathematics education in Washington State USA. There is now a […]
Pingback by Mathematics Weblog » Dumbing Down 2 — Saturday 14 April 2007 10:42 am #