Diagonal Stripes in Group Table

Tuesday 14 August 2007 at 3:42 pm | In Articles | 5 Comments

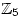One of my student’s attention was drawn to the fact, that in cyclic groups of order 4 and 5, it is possible to arrange the elements so that the transverse diagonals (that is those perpendicular to the leading diagonal) of the group (Cayley) table consist of equal elements. The groups in question were \mathbb{Z}^*_5 with multiplication modulo 5 and \mathbb{Z}_5 with addition modulo 5. Thus you get the following diagonal patterns highlighted by the colours:

\begin{array}{c|cccc} \times_5 & 1 & 2 & 4 & 3 \\ \hline 1 & 1 & \color{green}2 & \color{red}4 & \color{blue}3\\ 2 & \color{green}2 & \color{red}4 & \color{blue}3 & 1\\ 4 & \color{red}4 &\color{blue}3 & 1 & \color{green}2\\ 3 & \color{blue}3 & 1 & \color{green}2 & \color{red}4\\ \end{array} \qquad\qquad \begin{array}{c|cccccc} +_5 & 0 & 1& 2 & 3 & 4 \\ \hline 0 & 0 & \color{green}1 & \color{red}2 & \color{blue}3 & \color{magenta}4 \\ 1 & \color{green}1 & \color{red}2 & \color{blue}3 & \color{magenta}4 & 0 \\ 2 & \color{red}2 &\color{blue}3 & \color{magenta}4 & 0 & \color{green}1\\ 3 & \color{blue}3 & \color{magenta}4 & 0 & \color{green}1 & \color{red}2\\ 4 & \color{magenta}4 & 0 & \color{green}1 & \color{red}2 & \color{blue}3 \end{array}

He asked 2 questions:

1. Can the elements of all (finite) cyclic groups be arranged to give these diagonal stripes?

If you take a finite cyclic group generated by the element 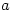a (we will use multiplication for the binary operation) then the natural ordering 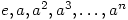e, a ,a^2 , a^3, \dots, a^n will show this pattern:

\begin{array}{c|llllllll} & e & a & a^2 & & & a^{i-1} & a^i & \\ \hline e & e & \color{green}a & \color{red}a^2 & & & & \color{blue}a^i \\ a & \color{green}a & \color{red}a^2 & & & & \color{blue}a^i \\ a^2 & \color{red}a^2 & & & &\color{blue}a^i\\ \\ a^{i-1} & & \color{blue}a^i\\ a^i & \color{blue}a^i\\ \\ a^{j-1} & & & & & & & \color{magenta}a^{j-1+i}\\ a^j & & & & & & \color{magenta}a^{j+i-1}\\ \ \end{array}

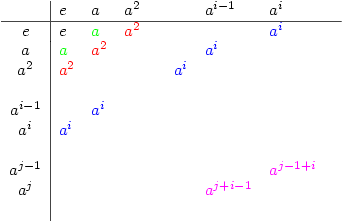
2. Are the cyclic groups the only ones that generate these patterns?

The answer is yes, but is not quite so obvious although not difficult to prove. Suppose a (finite) group G arranged as 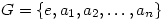G=\{e,a_1,a_2,\dots,a_n\} exhibits the diagonal stripes. Use induction. Let 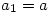a_1=a and suppose also that 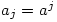a_j=a^j for 1 \le j<i. Then we get:
\begin{array}{c|lllllll} & e & a & & & a_{i-1} & a_i & \\ \hline e & & & & & & \color{blue}a_i & \\ a & & & & & \color{blue}aa_{i-1} & \\ \ \end{array}
It follows that 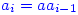\color{blue}a_i=aa_{i-1} so by induction assumption, 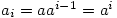a_i=aa^{i-1}=a^i and hence 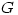G is the cyclic group generated by a.

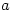5 Comments

TrackBack URI

  1. nice post. welcome back!
    (i had you listed as “inactive”
    for a while there since you
    hadn’t posted in a while …)

    it might interest you to know
    (in light of a comment of yours
    made in the “math blogs” post)
    that an “isabel” is blogging math
    (do doing a darn good job *of* it) at
    http://godplaysdice.blogspot.com/
    .

    Comment by vlorbik — Wednesday 15 August 2007 1:49 pm #

  2. I wonder if it is the Isabel whose old blog is preserved here?

    Comment by steve — Wednesday 15 August 2007 3:06 pm #

  3. Nice problem and interesting observation! This is something I noticed offhand but never bothered to sit down and look at properly.

    Comment by Dave — Sunday 19 August 2007 10:07 pm #

  4. It is a nice question. What I really enjoyed though, and sometimes I don’t think about it, is how automatically math folks ask the follow up question.

    In this case, I knew the answer to the first, but had never thought about the converse. Induction? Worked nice, I am out of practice and wouldn’t have jumped to it.

    I’d like my students to get some feeling for asking the follow ups: “how can we extend this?” “is there another question we can ask?” “can we generalize?” “is this always true?” “is this ever true?” and of course, “is the converse true as well?”

    Comment by Jonathan — Wednesday 22 August 2007 3:01 am #

  5. Another question which one of my lecturer encourages us to ask is, “If a condition of the theorem was removed what then?” Or something similar. (Eg. I think it was the inverse function theorem, and a possible question was what if the function is not strictly monotonic?)

    (I actually understand this post now! Well I get the theory, but need to revise definitions etc…)

    Comment by beans — Thursday 13 December 2007 8:57 pm #

Sorry, the comment form is closed at this time.

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^