Mathematics Weblog
Dumbing Down 2
Saturday 14 April 2007 at 10:42 am | In Articles | 8 CommentsIn Dumbing Down I mentioned the concern about mathematics education in Washington State USA. There is now a campaign there about ‘reform math’ which appears to be a system of education that tries to avoid teaching mathematics skills. As part of the campaign you can watch videos on YouTube from meteorologists Math Education: An Inconvenient Truth (which unfortunately stops half-way through) and Math Education: A University View. The latter video claims that California abandoned ‘reform math’ some years ago and as a result had an astonishing increase in students’ mathematical performances. You can read more on the campaign’s website Where’s the Math?
I shall be following this debate because, where the US goes, the UK often follows. This dumbing down of mathematical education may be linked to the shortage of good mathematics teachers since such ‘reform math’ can be taught by non-mathematicians. It’s clear that the descent into a downward spiral soon follows.
In the UK there has been a suggestion of ‘bribing’ students to study maths and science A levels ‘Pay students’ to revive science – are today’s students that shallow? How about good mathematics teaching which imbues a sense of wonder and delight?
 Alexandre Borovik in Division of Labour suggests that
The era of extensive mathematical education of majority is over — we have to develop a model of intensive mathematical education of minority.
He is not convinced that the mathematical education community can do this. I like the idea of extending the syllabus for those students who have the ability but I am also concerned about not leaving mathematics to an elite totally cut-off from the rest of the country.
 Hence my previous question in Dumbing Down
Is it possible to teach mathematics to a larger range of students without compromising on the level taught?
PS I just have to add this quote from The Unapologetic Mathematician discussing this issue because it encapsulates what I have been trying to say for years though I fear it fell on deaf ears
The algorithm comes first, and understanding comes later. Mathematics simply is. It cannot be negotiated. Mathematics education as realized in the NCTM standards has been taken over by sociologists, or even Critical Theorists. They are vehemently opposed to the seemingly-authoritarian rote method and saying “just do it like this and don’t ask whyâ€. Never mind the fact that in this case “why†comes naturally after “howâ€. And it’s about time for mathematicians to come down and start kicking some ass over this, or we’ll be left with nobody capable of replacing us.
Another Chance to Read … Calendars
Monday 2 April 2007 at 1:56 pm | In Articles | 4 CommentsIt’s not just television that thrives on repeats; I thought it worth repeating a posting about calendars from a year ago …Â
It is this time of year that has attracted a lot of attention devoted to finding the dates of religious festivals. A very comprehensive calendar calculator for 25 different calendar systems can be found at Calendrica (Java applet) and details of these systems are given in a fascinating book Calendrical Calculations.
Algorithms to calculate Easter dates have been given by mathematicians through the ages, including Gauss (see for example Mind Over Mathematics: How Gauss Determined The Date of His Birth) but it does produce a few errors. In 1961 the Scottish mathematician T.H. O’Beirne published an algorithm in his Puzzles and Paradoxes column in the New Scientist subsequently reprinted in his book of the same name published by the Oxford University Press (sadly out of print but I throughly recommend looking for a second-hand copy).
O’Beirne’s algorithm (based on an 1876 article in Nature) has the merit of always giving the correct date as well as being easy to use. It is a simple exercise to write a program to do the work for you. Simple Example
O’Beirne’s algorithm
The following process gives the date of Easter Sunday as the 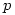 th day of the
th day of the  th month in year
th month in year 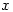 . It also gives the Golden Number
. It also gives the Golden Number 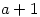 and the epact (
and the epact (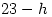 or
or 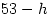 whichever is between 1 and 30 inclusive). All you have to do is start with the year
whichever is between 1 and 30 inclusive). All you have to do is start with the year 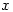 and perform 10 division operations noting the quotients and remainders.
and perform 10 division operations noting the quotients and remainders.
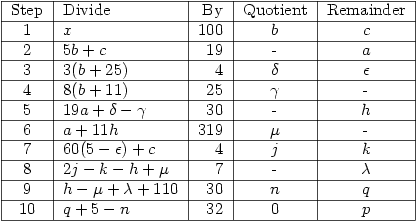
(Table produced by LaTable)
Dumbing Down
Thursday 29 March 2007 at 12:47 pm | In Articles | 4 CommentsThere’s a fascinating post at The Unapologetic Mathematician called Math and science testing in public schools which says that, because many students are failing the current maths and science tests, Washington state is proposing that they should be replaced by easier end of course tests:
I went to public schools in Maryland, where we had similar exams. Those students sharing my cynical bent referred to them as the “functional idiot testsâ€. I really do mean that it mostly tested respiratory function. I passed two of them by filling in pseudorandom bubbles and never actually opening the test booklet.
This picture of dumbing down will be familiar to British readers. This quote from the same post
This is exactly what Washington state is about to do. The important thing is evidently not to teach mathematics or science to its students. It’s to draw the target after we know where they land — give them a test we know they can pass.
echoes some of the controversy over new GCSE Science exams to be taken by 16 year olds Critics attack new science GCSE. I have never met any mathematics teacher who isn’t convinced that mathematics in the UK has been dumbed down quite considerably. The one attempt in 2000 to redress this problem ended in miserable failure and so the slide downwards has continued.
But there’s another issue here. In Britain, over at least the last 100 years or more, there has been an attempt to democratise education in the sense that, where only elites stayed on at school beyond the age of 14 in the early 20th century, there are proposals to raise the school leaving age to 18 and ensure that 50% of the population go on to higher education. It means that studying mathematics is compulsory at least until the age of 16.
This is good but the effect has been to simplify the syllabus substantially to allow more students to succeed. Examination questions set in the early twentieth century on complicated algebraic manipulation or a question on inversion (see * below) set in 1962 could not be set now. So the question that needs to be asked is
Is it possible to teach mathematics to a larger range of students without compromising on the level taught?
Alexandre Borovik’s book Mathematics under the Microscope in the section 4.6 Mental arithmetic and the method of Radzivilovsky details a radical approach by “a brilliant and idiosyncratic mathematics teacher, Vladimir Radzivilovsky” who
systematically builds bridges between various mental presentations of order and number in his pupils’ heads
and
Radzivilovsky’s success is measured by the fact that, among his former students, he can name dozens of professional mathematicians, physicists and computer scientists
There must be others who have ideas about teaching mathematics to a wide range of students whilst still maintaining standards.
* Here is an inversion question taken from a University of London A level Paper III Summer 1962:
Prove that the inverse of the point
with respect to the circle
is
Find the equations of the inverses of the circles
and
with respect to the circle
.
Deduce that
and
intersect at right angles.
How To Write Mathematics Badly 3
Friday 16 March 2007 at 4:44 pm | In Articles | 8 CommentsMost of the advice on writing mathematics in the previous posts is aimed at the postgraduate student or those writing papers. Yet many of us are all too keenly aware that undergraduate students are in even greater need of help. For example,
- misuse of the equals sign; I’ve lost count of the number of times have I told students that both sides of = must be of the same type so a function doesn’t equal a point in
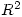 and ‘equals’ is not a synonym of ‘therefore’ or ‘implies’;
and ‘equals’ is not a synonym of ‘therefore’ or ‘implies’; - sentences that are missing one or more of subject, verb, object;
- steps in a proof that have no relation to what has gone before;
- etc …
I am pleased to say that Dr Kevin Houston of Leeds University has written to me to tell me how he is trying to help students to write properly:
- I am writing a book called How to Think Like a Mathematician which includes a bit about writing mathematics at university (but can be applied at lower levels). This is aimed at first degree students – I notice that a lot of advice about writing maths is aimed at PhD students, for example, the video of Serre.
The sample chapter on writing is on my website along with the full booklet that we give to our first year maths students here at Leeds.
A couple of quotes taken at random:
- An equation involves saying that two expressions are equal, for example,
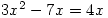 . Note that an inequality, such as
. Note that an inequality, such as 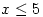 , is not an equation.
, is not an equation.
‘The number of people over 40 = 5’, which reads all right, but the eye is drawn to the (erroneous) expression 40 = 5.
Well-worth reading!
How To Write Mathematics Badly 2
Tuesday 27 February 2007 at 12:30 pm | In Articles | 1 CommentIn the previous post I linked to a video lecture by Jean-Pierre Sierre on writing mathematics. However I should also have linked to a series of lectures on Mathematical Writing by Donald Knuth and others given nearly 20 years ago in the Autumn of 1987 at Stanford University. To quote from Don Knuth: Musings and More “I also gave a class called Mathematical Writing, just for one quarter,” says Knuth. “The lectures are still of special interest because they feature quite a few important guest lecturers.” This collection contains thirty-one tapes. If you haven’t got the time to sit through all the videos you can download a transcript of the course (or buy the book) in plain TeX format on Donald Knuth’s site: Mathematical Writing
On a slightly different tack there are a couple of papers on mathematical research that would be useful to postgraduate students:
- Advice to the beginner by Alain Connes
- What is good mathematics? by Terence Tao Some personal thoughts and opinions on what “good quality mathematics” is, and whether one should try to define this term rigorously. As a case study, the story of Szemerédi’s theorem is presented.
I’d be very interested if there are any more online resources on mathematical writing or beginning research.
Thanks to Noncommutative Geometry for the links to the two papers above.
PS Gooseania has mentioned that Nick Higham’s Handbook of Writing for the Mathematical Sciences is good.
eon mentions Some Hints on Mathematical Style by David Goss which has been recently updated with suggestions by Jean-Pierre Serre. It contains a number of references to other papers and books on writing style.
How To Write Mathematics Badly
Monday 26 February 2007 at 10:36 pm | In Articles | 5 CommentsJean-Pierre Serre (and also see Wikipedia) is one of the most eminent mathematicians alive; he was part of Bourbaki in the later stages, and he has been awarded many mathematical prizes. So it is a pleasure to watch a video of him explaining how to write good mathematical papers. He does this by explaining how to not to write mathematics which is why his talk is entitled How To Write Mathematics Badly.
You can forgive the amateurishness and poor sound quality of the 56-minute video for the sageness of the advice he gives. I don’t know when the talk was given but if it was recent he is doing very well for a man in his eighties.
You can find the video on Google video at Jean-Pierre Serre – How To Write Mathematics Badly and is a must see for postgraduate students who appear to make up the bulk of the audience.
Thanks to ComplexZeta for the link.
Mathematics Blogs
Tuesday 13 February 2007 at 4:04 pm | In Articles | 10 CommentsThe number of maths blogs has risen dramatically in the last year, I am delighted to say. It started just a few years ago when Isabel’s math blog was one of the few (though sadly it has now vanished) to today when we there are thousands out there. Whether it is undergraduates blogging like Me Or My Maths, postgrads like Gooseania or professor (in the British sense so higher status than a lecturer) at Mathematics under the Microscope, all at Manchester University.
There are blogs like NeverEndingBooks which covers advanced topics like Noncommutative Geometry as well as being in the forefront of technical innovations (he is currently converting to using MathML and has a command line version which is fascinating). Then there are large collections of maths related blogs such as those at Art of Problem Solving and the huge number of blogs by Warwick University students and staff at Warwick Blogs.
Many such blogs deal with the writer’s experiences but if it is mathematics you are after then a good place to start is at Carnival of Mathematics: Inaugural Edition. This has links to mathematics blogs at all levels, such as mathematics quotes, mathematical objects like Klein bottles that you can buy, a hotly debated probability paradox (well worth reading for an insight into the intricacies of this subject) all the way up to group cohomology. Do visit Carnival of Mathematics: Inaugural Edition – you may never have time to read anything else once you’ve explored the links and the links to the links … 🙂
One final thing – the vast majority of mathematics blogs I have come across use WordPress or Google’s Blogger. I expect this is true of most blogs in all subjects, though WordPress is particularly suitable for mathematics because of the LatexRender plugin allowing maths notation. If you wish to generate your own mathematical images but don’t have access to 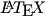 then have a look at the online LaTeX Equation Editor. You can also download the source code which uses a mix of Ajax, JavaScript, PHP, HTML and
then have a look at the online LaTeX Equation Editor. You can also download the source code which uses a mix of Ajax, JavaScript, PHP, HTML and 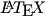 .
.
“Mathematics” vs Mathematics
Tuesday 23 January 2007 at 12:04 pm | In Articles | 2 CommentsA link in one of the comments at Mathematics dying on the vine in Australian universities drew my attention to a paper called “Mathematics†vs Mathematics by I. Bokor of the School of Mathematics, Statistics and Computer Science, University of New England, Armidale NSW. This paper attempts to dispel some myths such as:
- The view seems to be commonly held, even amongst mathematics and science educationists, that mere passing familiarity with rudimentary facts is more than adequate for teaching these subjects at school. School teachers, and even those who train them, frequently argue that it is actually preferable to know less about mathematics and science in order to teach them better.
There is a confusion of numeracy with mathematics, a fallacy as crude as equating literacy with literature. For while one must be numerate in order to attempt to learn or appreciate mathematics, there is a qualitative difference between mathematics and mere computation, just as a narrative text does not become literature solely because it is free of grammatical errors and spelling mistakes.
Partly as a consequence, there is a pervasive belief, including among those who use and apply mathematics, that any mathematical problem has a unique solution, which can be readily computed numerically if one just had the right computer with the right programme, or, failing that, by being adept enough.
If I had not experienced this myself I wouldn’t have believed that these myths are all too common these days. The author illustrates the difference between mathematics (the reality) and “mathematics†(the myth) by discussing the mathematics involved in answering a supposedly simple problem like  .
.
A paper worth reading.
Mathematics in Crisis
Monday 22 January 2007 at 11:54 pm | In Articles | 3 CommentsThose of us who live and work in the UK are worried about the crisis in mathematics in this country, both in schools and universities. It appears that there are similar problems in Australia as described in Mathematics dying on the vine in Australian universities. As Alexandre Borovik of Mathematics under the Microscope, who pointed me to the post, says (well almost, I’ve slightly altered what he wrote)
- We continue to underestimate the gravity of the crisis of mathematical, and, more generally, scientific education [in] Western civilization.
So the question is What are we going to do about it?
Mathematics is different
Thursday 11 January 2007 at 9:38 pm | In Articles | Post CommentTwo blog posts have caught my eye. The first is Time Lag in Learning Mathematics which talks about the time it takes for a student to learn mathematics followed by the observation that one cannot be said to understand a topic until one can apply it. This often only occurs in the year after one has learnt the subject which is why I often tell my university students that it will always be true that Last year’s course was easy, this year’s is hard and next year’s is impossible.
A very important point that Mathematics under the Microscope makes is that anyone teaching mathematics should have a qualification at least one level higher than that being taught.
It is so hard to convince non-mathematicians that teaching and learning mathematics is very different from most other subjects. This partly accounts for the appalling state of teacher training and observation in the UK and why I absolutely refused to be judged by unqualified observers.
In the second post the secret life of numbers gives a quote from the book it is discussing which gives a better alternative to a question I often ask Why are people happy to admit to being innumerate but prefer to hide their illiteracy? PS Mathematics under the Microscope has an interesting response to this.
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^