Mathematics Weblog
Royal Institution Lectures
Tuesday 19 December 2006 at 2:34 pm | In Articles | 3 CommentsFor only the third time in its history the Royal Institution Christmas Lectures will be on mathematics. Marcus du Sautoy, who was inspired by the first mathematics lectures given by Christopher Zeeman in 1978, will be presenting The Number Mysteries. They will be broadcast on Channel Five.
The previous Christmas lectures on Mathematics were given by Ian Stewart in 1997.
There’s an interview with Marcus du Sautoy in today’s Guardian called A prime example.
Laugh or cry?
Monday 11 December 2006 at 2:35 pm | In Articles | 1 CommentI feel bound to add to the viral blogging* publicising a highly amusing phone call made by a chap querying the bill from an internet provider. The company insists that it charges 0.002 cents per KB and that using 35 893 KB costs $71.79. The phone call is an attempt to persuade the company that they are out by a factor of 100. It is a conversation with employees, who are remarkably patient, but think 0.002 cents = 0.002 dollars.
I have to say I laughed a lot but maybe I should cry at the lack of mathematical ability.
You can find the recording at Tragicomic Mathematics and click on recording. It lasts just under half-an-hour. The comments on that page are also amusing particularly the one where the manager asks for “Not a percent of anything, just a plain percent“.
* Ketcheson.net says:
- On Thursday, someone named “georgevaccaro” create a blog called VerizonMath. In it, he details a bizarre serious of conversations he has had with Verizon revolving around the per KB charges he incurred while accessing data on his phone during a trip to Canada. He was quoted a rate of “.002 cents per KB”, when in fact the customer service representatives had actually meant “.002 dollars per KB.” On his blog, he documents his interactions with the company, posts up a (very funny) audio file of his phone conversation, and he also uploaded a copy of the same phone call to Youtube.
This has spread with the typical speed of a hot blogstorm. His blog has pulled in more than 20K hits, the Youtube video has upwards of 45K views, and the blog has been linked to by more than 300 other blogs. This is going to get much worse before it gets better, and the image it has created of Verizon customer service couldn’t be much more negative.
There’s a very funny Wikipedia entry on this topic here.
Thanks to Mathematics Under the Microsocope
Mathematics in the real world
Thursday 7 December 2006 at 3:46 pm | In Articles | 1 CommentMathematics is often thought of as being esoteric and nothing to do with the real world which, to be honest, is why it appealed to me when I decided to study maths at University. However, I am delighted to see that the subject of toilet seats (up or down?) has been tackled by Hammad Siddiqi in a paper called The social norm of leaving the toilet seat down: A game theoretic analysis. Some extracts give the flavour:
- In this paper, we internalize the cost of yelling and model the conflict as a non-cooperative game between two species, males and females. We find that the social norm of leaving the toilet seat down is inefficient. However, to our dismay, we also find that the social norm of always leaving the toilet seat down after use is not only a Nash equilibrium in pure strategies but is also trembling-hand perfect.
[…]
Changing the seat position during an operation is beyond the scope of this paper and is definitely not recommended.
[…]
In this paper, we show conclusively that the social norm of leaving the toilet seat down after use decreases welfare and by doing that we hope to convince the reader that social norms are not always welfare enhancing. Hence, there is a case for scientifically examining social norms and educating the masses about the fallacy of following social norms blindly.
Ars Mathematica first alerted me to this paper, but it has spread virally from blog to blog. I have alerted the Annals of Improbable Research so hopefully it will receive a wider audience. The editor contributes a weekly column in the Guardian; this week’s column is subtitled “The dangers of whisky and candlelight”.
Mathematics Under The Microscope
Friday 24 November 2006 at 2:25 pm | In Articles | 2 CommentsMathematics under the Microscope by Alexandre V. Borovik is a new book looking at mathematics, how it works, what happens in the brain when it does mathematics and, using this knowledge, discusses how it should be taught. It is the last part that particularly interests me since so little is understood in this country about mathematical education. We have an ever worsening system of mathematics in schools and colleges for which the blame must lie at the door of those non-mathematicians who think they know how it should be taught. Indeed I refused entry to my classes to anyone who was not a student or who had good mathematics qualifications or who had not read and understood my polemic enough to argue coherently with me about what I had said. There is far too much amateurism in the management of mathematics teaching and today’s Times Higher Education Article Johnson acts to halt closures shows the consequences. I was privileged to be able to teach many international students and it became obvious how far we had fallen behind in this country.
But this article is not supposed to be about my views but to celebrate Mathematics under the Microscope’s contribution to the debate; incidentally it has the important bonus that the author is able to bring to the discussion the benefits of a Russian mathematical education.
It is difficult to convey the scope of the book so I will resort to quoting parts of the author’s overview:
- I look at simple, minute activities, like placing brackets in the sum a + b + c + d + e.
- I analyze everyday observations so routine and self-evident that their mathematical nature usually remains unnoticed: for example, when you fold a sheet of paper, the crease for some reason happens to be a perfect straight line.
- I use palindromes, like MADAM, I’M ADAM, to illustrate how mathematics deals with words composed of symbols—and how it relates the word symmetry of palindromes to the geometric symmetry of solid bodies.
- I even discuss the problem of dividing 10 apples among 5 people!
[…]
In this book, I argue that we cannot seriously discuss mathematical thinking without taking into account the limitations of the information-processing capacity of our brain. In our conscious and totally controlled reasoning we can process about 16 bits per second. In activities related to mathematics this miserable bit rate is further reduced to 12 bits per second in addition of decimal numbers and to 3 bits in counting individual objects. Meanwhile the visual processing module of our brain easily handles 10,000,000 bits per second!
[…]
In my book, I am trying to respond to a sudden surge of interest in mathematics education which can be seen in the mathematical research community. It appears that it has finally dawned on us that we are a dying breed, that the very reproduction of mathematics as a social institution and a professional community is under threat. I approach the problems of mathematical education from this viewpoint which should not be easily set aside: what kind of mathematics teaching allows the production of future professional mathematicians? What is it that makes a mathematician? What are the specific traits which need to be encouraged in a student if we want him or her to
be capable of a rewarding career in mathematics? I hope that my observations and questions might be interesting to all practitioners and theorists of general mathematical education. But I refrain from any critique of, or recommendations for, school mathematics teaching. (my comment: which is a shame!)
[…]
When I read descriptions of some of the experiments in mathematical education, I wanted to call the NSPCC hotline and report child abuse.
[…]
… is a good example of why software based learning of mathematics is intrinsically flawed: the software forces on you a particular mode of visualization. However, visualization is too intimate a component of mathematical thinking to be entrusted to a computer.
To whet your appetite a little more here are a couple of the problems from Chapter 7: What Is It That Makes a Mathematician?
- Find a four-digit number with the following conditions: the product of the extreme digits is equal to 40; the product of the middle digits is 28; the thousands digit is as much less than the units digit as the hundreds digit is less than the tens digit; and if 3, 267 is added to the unknown number, the digits of the number are reversed.
- Here are several dates in Swahili:
tarehe tatu Disemba jumamosi; tarehe pili Aprili jumanne; tarehe nne Aprili jumanne; tarehe tano Octoba jumapili; tarehe tano Octoba jumatatu; tarehe tano Octoba jumatano.
The translations in English are given in random order:
Monday 5 October; Tuesday 2 April; Wednesday 5 October; Sunday 5 October; Saturday 3 December; Tuesday 4 April.
Write in Swahili:
Wednesday 3 April; Sunday 2 December; Monday 1 November.
The book is unusual in that you can download it free under a Creative Commons licence and this also has the advantage that the author can and does update and amend it. Indeed he welcomes comments. Do be aware though that the references are also being updated & renumbered so may get out of synch with a previous version you may have printed out.
The Transcendence of 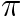
Friday 10 November 2006 at 3:35 pm | In Articles | 9 Comments
Many people have seen the proof that 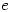 is irrational (eg e is irrational); fewer have read the proof that
is irrational (eg e is irrational); fewer have read the proof that 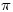 is irrational (eg Pi is irrational) but how many have seen the proofs that
is irrational (eg Pi is irrational) but how many have seen the proofs that 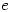 and
and 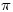 are transcendental ie not the solution of any polynomial in integer (or rational) coefficients? It’s a shame as these results are fascinating and are easily accessible to degree level students.
are transcendental ie not the solution of any polynomial in integer (or rational) coefficients? It’s a shame as these results are fascinating and are easily accessible to degree level students.
Of course, if you are willing to accept Lindemann’s result that if 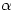 is algebraic then
is algebraic then 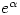 is transcendental, then the fact that
is transcendental, then the fact that 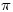 is transcendental follows immediately from the transcendence of
is transcendental follows immediately from the transcendence of 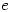 (click on read more below if you can’t see why).
(click on read more below if you can’t see why).
But that’s silly as Lindemann’s theorem is hard to prove. However, I have some notes, typed out on green banda sheets. They were a supplement to a course given by Ian Stewart back in the long forgotten past, well, 1970 to be precise. Very good they are too. I have LaTeXed them and you can read the proofs yourself here: The Transcendence of Pi.
Ian Stewart said (and I agree with him) that back in 1970, a student just needed to understand first-year undergraduate analysis to follow the proofs. I wonder if that is still true?
Continue reading The Transcendence of 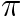 …
…
Don’t Miss This!
Saturday 28 October 2006 at 6:26 pm | In Articles | Post CommentFrom Mathematics Under The Microscope:
- On Thursday, 2 November, in the programme In Our Time on BBC Radio 4 (9.00-9.45am, repeated 9.30pm), Melvyn Bragg and guests will discuss Poincare Conjecture.
It will also be available on Listen Again for a further week after the broadcast.
Mathematics is hard
Tuesday 24 October 2006 at 10:43 am | In Articles | 3 CommentsA number of blogs have picked up on a US report that says:
- that countries with students who say they enjoy mathematics scored much lower than countries that rank lower in mathematics enjoyment
The nations with the best scores have the least happy, least confident math students
We might want to focus on the math that kids are learning and just be a little less obsessed with the fact that they have to enjoy every minute of it
Other countries do better than the United States because they seem to expect more from students. That could also explain why high performers in other nations express less confidence and enjoyment in math. They consider their peer group to be star achievers.
Even efforts to make math relevant may be irrelevant, says the study
Nations that try to teach math in terms of daily life have the lowest test scores.
(the full report is available here)
These ideas may seem astonishing, yet to many battle-scarred maths teachers it is what they have been saying for years. Mathematics is hard and it requires dedication, effort and time to understand it. This is not popular so in the UK we have decided to get round the problem by making the subject easier, delivering it in small easily-digestible lumps and as formulaic as possible so anyone can follow it. To prove we are delivering (ha!) we test and re-test making sure that the questions we set are virtually identical each year and again, divide up into little pieces.
It’s a bit like teaching someone to ride a bike by ensuring that they always use stabilisers. Learning to maintain balance takes lots of time and practice and the same is true of mathematics. Yet in the end we lose out. The cyclists never discover the excitement and freedom of cycling alone and the mathematics student never discovers the beauty of mathematics, forever imprisoned by having to apply the same tedious but not understood methods to the same problems.
Ian Stewart in Concepts of Modern Mathematics puts it this way:
- the technical grind is not just an afterthought: it is an absolutely essential part of the process … The problem with the hard technical grind is that there is no way to appreciate it except by doing it … If we can get away from the alarming habit that has grown up of shying away from anything that is the least bit difficult, then we may make real progress.
Mathematics is hard and we do ourselves a disservice by denying or avoiding it. More, not less, time should be devoted to it in schools and colleges so that students have time to practice and have the opportunity to really think; only then will come understanding.
You can (and should) read more about this topic at
Mathematics Under the Microscope
NeverEndingBooks (from Belgium, top western country for mathematics according to a survey on which the report is based)
The Reference Frame
You may wish to contribute to this discussion on Gooseania’s blog.
PS Today’s Education Guardian has an article Four steps to being chucked on the scrapheap which describes the problems that arise with the formulaic approach to teaching any subject. The author, an experienced teacher, writes very well. I have always said that OFSTED inspired teaching plans are bollocks but now I can put it so much better and say
- a lesson plan goes together with good teaching like a horse and gherkin
Stretching Question 2
Friday 13 October 2006 at 3:14 pm | In Articles | 3 CommentsIn Stretching Question I wondered how students would cope with a type of question they wouldn’t have seen before:
- If
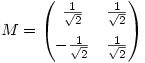 calculate
calculate 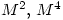 and
and 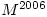
The examiners’ report is now out and it says (edited to show context)
- Attempts at calculating
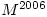 were rarely completely successful. Many candidates found that
were rarely completely successful. Many candidates found that 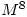 was the identity matrix but then went on to say that
was the identity matrix but then went on to say that 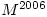 must also be the identity matrix. Others gave the value of
must also be the identity matrix. Others gave the value of 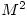 or gave the correct answer without any indication as to their reason for doing so, or with incomplete reasoning.
or gave the correct answer without any indication as to their reason for doing so, or with incomplete reasoning.How disappointing that so few managed to complete the question successfully. The lack of reasoning doesn’t tell us whether students guessed or found it too easy to bother putting down the working. It might have helped if students were taught that if 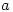 and
and 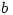 are integers then there exist integers
are integers then there exist integers 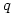 and
and 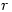 with
with 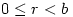 such that
such that 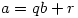 but these fundamental ideas seemed to have been lost to A level.
In the first AS exam the examiners comment that
but these fundamental ideas seemed to have been lost to A level.
In the first AS exam the examiners comment that
- When asked to use the Factor Theorem or Remainder Theorem, no marks can be earned for using long division.
which means
- British students haven’t a clue how to do long division of polynomials so we’ve made it easier for you, so don’t try and pretend you know best. (See A Level Exam Questions).
Blackboards
Tuesday 10 October 2006 at 1:45 pm | In Articles | Post CommentPress coverage has led me to Psychophysiology of Blackboard Teaching, Revisited which of course refers to the original article written in August. My only disappointment is that it is now too late to add anything useful to that article.
My experience in working in a College and for the Open University is that very few people understand anything about the teaching of mathematics. They seem to think that a few square centimetres of white board is sufficient and, nowadays, it can all be done ‘using a computer’ though those that say this can barely find the on-switch of a computer.
I have had battles in the past to get decent writing surfaces. I am happy with blackboards or whiteboards providing they provide very large surfaces. In fact they would have to be roller boards in order to accommodate the area I need. Even when you get what you want, few people think about maintenance so you end up with boards that are in a disgusting state and impossible to use. It helps if the previous user would clean the board after they have finished.
I don’t object to people being ignorant about how mathematics should be taught; what really gets me is their arrogance that they know best.
So good luck to Alexandre Borovik’s campaign! Do read Psychophysiology of Blackboard Teaching about the importance of blackboards in mathematics teaching.
Alternative Arithmetic
Sunday 8 October 2006 at 1:01 pm | In Articles | 1 Comment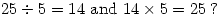 See Maths Lesson in the Mathematics Under the Microscope blog for a ‘proof’.
See Maths Lesson in the Mathematics Under the Microscope blog for a ‘proof’.
The film clip is amusing but just pause to think how much damage is done by non-specialist mathematics teaching. Good maths teachers should be nurtured and valued but they certainly aren’t in the UK. Grrr!
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^