Mathematics Weblog
This site uses LatexRender for the mathematics
More Trig Ratios
Monday 23 May 2005 at 9:42 pm | In Articles | 6 CommentsStudents studying A level mathematics are expected to know exact values of a few trig ratios such as 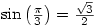 (see Trig Ratios posting). But a visit to Mathworld reveals a whole world of fascinating values.
(see Trig Ratios posting). But a visit to Mathworld reveals a whole world of fascinating values.
Here are just a few of them (you may wish to try proving them)
![\cos\left(\dfrac{\pi}{9}\right)=2^{-\frac{4}{3}}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right) \cos\left(\dfrac{\pi}{9}\right)=2^{-\frac{4}{3}}\left(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}}\right)](/maths/latexrender/pictures/582104b66f6cfb8d988b27f2b7d58ea5.gif)
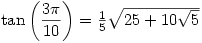
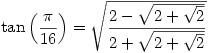
![\sin\left(\dfrac{\pi}{17}\right)=\frac{1}{8}\left[34-2\sqrt{17}-2\sqrt{2}\epsilon^*-2\sqrt{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\epsilon}\:\right]^{\frac{1}{2}} \sin\left(\dfrac{\pi}{17}\right)=\frac{1}{8}\left[34-2\sqrt{17}-2\sqrt{2}\epsilon^*-2\sqrt{68+12\sqrt{17}+2\sqrt{2}(\sqrt{17}-1)\epsilon^*-16\sqrt{2}\epsilon}\:\right]^{\frac{1}{2}}](/maths/latexrender/pictures/d96c38bb044f64eab33ac3dacf4b476a.gif)
where 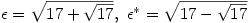
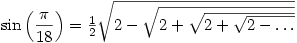 where the sequence of signs
where the sequence of signs 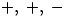 repeats with period 3
repeats with period 3
As I said, fascinating!
Thank goodness  can show these values easily!
can show these values easily!
6 Comments »
RSS feed for comments on this post. TrackBack URI
Leave a comment
Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds.
Valid XHTML and CSS. ^Top^
In re the first line: unless I’m missing some subtle joke, you want sin(45) to be sqrt(2)/2. Otherwise sin(45) is the same as sin(60), and this would make your unit circle lumpy.
Comment by Christian Claiborn — Tuesday 24 May 2005 4:16 pm #
Aaargh! How did that 4 get there? Corrected now. Thanks very much for pointing it out!
Comment by Steve — Tuesday 24 May 2005 5:38 pm #
Interesting note: you can use such results, together with the fact we know how to solve cubics/quartics explicitly, to prove that the sine of ONE degree (pi/180) is expressible as a radical!
Comment by Mr Blobby — Thursday 26 May 2005 12:21 am #
Why, I wonder, write (1/5)√(25+10√5)) rather than √(1+ 2/√5) ? … And why do my plus and minus signs vanish when I hit Preview?
Comment by Anton Sherwood — Tuesday 14 June 2005 5:44 am #
I have corrected the + sign bug, thanks for that
Comment by steve — Tuesday 14 June 2005 5:17 pm #
Well I did one exercise using complex numbers which helped me find the exact value of the cosine and sine of pi/12
with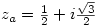 and
and 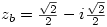
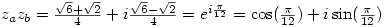
now
Comment by Luc — Friday 31 March 2006 5:53 pm #