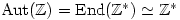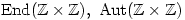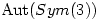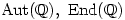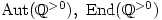A Levels

Monday 20 August 2007 at 11:38 am | In Articles | 12 Comments

Last Thursday the A level results were announced and there were the usual recycled comments with some people attacking and others defending the system. There appears to be three main arguments used:

  1. A levels are getting easier;
  2. Teachers are getting better at preparing students for the exams;
  3. Students work very hard and so it is insulting to them to say the exams are getting easier.

So let’s examine these arguments for A level maths, which is the subject I know about. Unlike some pundits I don’t wish to pontificate about subjects I am not familiar with. My main point is that the arguments above are not contradictory and it is quite possible for exams to be easier than in previous years and for students to find them hard.

  1. It is generally acknowledged in the mathematical community that A level maths exams are getting easier and it has been remarked on by a government advisor  A-levels are easier says adviser. Yet this headline is misleading because it is only referring to maths and physics which shows just how difficult it is to have a rational argument about the standard of A levels.
    It is interesting to see the effect this is having on university mathematics courses even in the last few years A-Levels: Gah. 
    However, A level mathematics and its equivalent has become steadily easier over at least the last hundred years as the subject has been ‘democratised’ and taught to a wider population. I am very much in favour of this but the cost has been the dumbing down of the syllabus as I have mentioned before. I can only repeat my question that

    Is it possible to teach mathematics to a larger range of students without compromising on the level taught?

  2. This is true but nothing to be proud about. Teachers and schools are under extraordinary pressure to get good results. Hence they teach very much to the exams, test and retest, and have no time to explore interesting parts of mathematics which would help to motivate and put things into context.
    How politicians can imply that this is good beats me.
  3. Mathematics, as those of us who taught it know, is hard. This has been recognised (finally) by recent research, and it has been proposed that, as happens in Australia, more UCAS points are awarded for harder subjects like maths, though I can’t see that it will happen here.
    Also mathematics is essentially linear so unless students are adequately prepared at one stage they will find it very difficult to proceed to the next stage. With dumbing down going right back to the early years of education most students will find each stage hard no matter what the level. The ignorance of this caused disaster in 2000 when A level maths was temporarily made tougher and so the gap from GCSE was unbridgeable for many students, leading to lots of failures, the abandonment of the subject by many and the restoration of an easier system.
    Finally, with a greater percentage of the student population studying mathematics many of them are bound to find the subject hard.

It is good that Further Mathematics is becoming more popular and is to be encouraged, though it should be noticed that it too is a pale reflection of when it was last popular.

I don’t have easy answers to the problems of mathematical education but wish to see an informed debate on it. I just hope that Alexander Borovik is not correct when he writes

The current crisis in mathematics teaching is a dawn of a much more serious crisis of transition from the mass mathematics education of the past to a more selective and elitist education of increasingly small, in relative terms, numbers of mathematicians.

Diagonal Stripes in Group Table

Tuesday 14 August 2007 at 3:42 pm | In Articles | 5 Comments

One of my student’s attention was drawn to the fact, that in cyclic groups of order 4 and 5, it is possible to arrange the elements so that the transverse diagonals (that is those perpendicular to the leading diagonal) of the group (Cayley) table consist of equal elements. The groups in question were \mathbb{Z}^*_5 with multiplication modulo 5 and \mathbb{Z}_5 with addition modulo 5. Thus you get the following diagonal patterns highlighted by the colours:

\begin{array}{c|cccc} \times_5 & 1 & 2 & 4 & 3 \\ \hline 1 & 1 & \color{green}2 & \color{red}4 & \color{blue}3\\ 2 & \color{green}2 & \color{red}4 & \color{blue}3 & 1\\ 4 & \color{red}4 &\color{blue}3 & 1 & \color{green}2\\ 3 & \color{blue}3 & 1 & \color{green}2 & \color{red}4\\ \end{array} \qquad\qquad \begin{array}{c|cccccc} +_5 & 0 & 1& 2 & 3 & 4 \\ \hline 0 & 0 & \color{green}1 & \color{red}2 & \color{blue}3 & \color{magenta}4 \\ 1 & \color{green}1 & \color{red}2 & \color{blue}3 & \color{magenta}4 & 0 \\ 2 & \color{red}2 &\color{blue}3 & \color{magenta}4 & 0 & \color{green}1\\ 3 & \color{blue}3 & \color{magenta}4 & 0 & \color{green}1 & \color{red}2\\ 4 & \color{magenta}4 & 0 & \color{green}1 & \color{red}2 & \color{blue}3 \end{array}

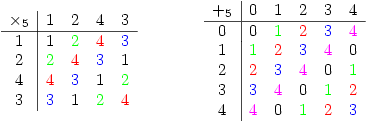
He asked 2 questions:

1. Can the elements of all (finite) cyclic groups be arranged to give these diagonal stripes?

If you take a finite cyclic group generated by the element 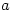a (we will use multiplication for the binary operation) then the natural ordering 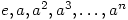e, a ,a^2 , a^3, \dots, a^n will show this pattern:

\begin{array}{c|llllllll} & e & a & a^2 & & & a^{i-1} & a^i & \\ \hline e & e & \color{green}a & \color{red}a^2 & & & & \color{blue}a^i \\ a & \color{green}a & \color{red}a^2 & & & & \color{blue}a^i \\ a^2 & \color{red}a^2 & & & &\color{blue}a^i\\ \\ a^{i-1} & & \color{blue}a^i\\ a^i & \color{blue}a^i\\ \\ a^{j-1} & & & & & & & \color{magenta}a^{j-1+i}\\ a^j & & & & & & \color{magenta}a^{j+i-1}\\ \ \end{array}

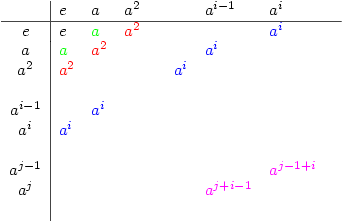
2. Are the cyclic groups the only ones that generate these patterns?

The answer is yes, but is not quite so obvious although not difficult to prove. Suppose a (finite) group G arranged as 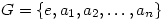G=\{e,a_1,a_2,\dots,a_n\} exhibits the diagonal stripes. Use induction. Let 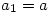a_1=a and suppose also that 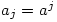a_j=a^j for 1 \le j<i. Then we get:
\begin{array}{c|lllllll} & e & a & & & a_{i-1} & a_i & \\ \hline e & & & & & & \color{blue}a_i & \\ a & & & & & \color{blue}aa_{i-1} & \\ \ \end{array}
It follows that 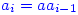\color{blue}a_i=aa_{i-1} so by induction assumption, 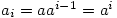a_i=aa^{i-1}=a^i and hence 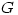G is the cyclic group generated by a.

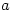Mathematics Summer School in Sirince in Turkey

Saturday 4 August 2007 at 11:15 am | In Articles | 2 Comments

Those of us involved in mathematics education often whinge about current standards, the lack of enthusiasm in students etc so it is refreshing to read Alexander Borovik’s reports Gold Sand in a Stream and Photos from Mathematical Village about a mathematics summer school for undergraduate students in Sirince in Turkey. The summer school was run by Professor Ali Nesin, who is  Chair of the Department of Mathematics of the Istanbul Bilgi University. Professor Borovik was enchanted not just by the beautiful setting but also by the ‘bright motivated students’.

The level of education was high including a crash course in reflection groups. One of the blackboards photographed includes the following mathematics:

If G is a group then the set \text{Aut}(G) of automorphisms of G forms a group under composition. If A is abelian then \text{Aut}(G)\subset \text{End}(A) .
\text{Aut}(\mathbb{Z})=\text{End}(\mathbb{Z}^*)\simeq \mathbb{Z}^*

Homework:
Find
\text{End}(\mathbb{Z}\times \mathbb{Z}), \ \text{Aut}(\mathbb{Z}\times \mathbb{Z})
\text{Aut}(Sym(3))
\text{Aut}(\mathbb{Q}),\ \text{End}(\mathbb{Q})
\text{Aut}(\mathbb{Q}^{>0}),\ \text{\text{End}}(\mathbb{Q}^{>0})
Show that if G\simeq H then \text{Aut}(G) \simeq \text{Aut}(H)  

But then the story goes sour. The authorities have closed the summer school – see A Blackboard under Arrest, A Blackboard under Arrest, II  – which is such a shame. There is a petition to save the school at Save Mathematical Summer School you may wish to support, but also, can I ask other bloggers, mathematical or otherwise, to spread the news in the hope that it will help find some way round the problem?

Powered by WordPress with Pool theme design by Borja Fernandez.
Entries and comments feeds. Valid XHTML and CSS. ^Top^