Mathematics Weblog

Dumbing Down 2

In Dumbing Down I mentioned the concern about mathematics education in Washington State USA. There is now a campaign there about ‘reform math’ which appears to be a system of education that tries to avoid teaching mathematics skills. As part of the campaign you can watch videos on YouTube from meteorologists Math Education: An Inconvenient Truth (which unfortunately stops half-way through) and Math Education: A University View. The latter video claims that California abandoned ‘reform math’ some years ago and as a result had an astonishing increase in students’ mathematical performances. You can read more on the campaign’s website Where’s the Math?

I shall be following this debate because, where the US goes, the UK often follows. This dumbing down of mathematical education may be linked to the shortage of good mathematics teachers since such ‘reform math’ can be taught by non-mathematicians. It’s clear that the descent into a downward spiral soon follows.

In the UK there has been a suggestion of ‘bribing’ students to study maths and science A levels ‘Pay students’ to revive science – are today’s students that shallow? How about good mathematics teaching which imbues a sense of wonder and delight?

 Alexandre Borovik in Division of Labour suggests that

The era of extensive mathematical education of majority is over — we have to develop a model of intensive mathematical education of minority.

He is not convinced that the mathematical education community can do this. I like the idea of extending the syllabus for those students who have the ability but I am also concerned about not leaving mathematics to an elite totally cut-off from the rest of the country.

 Hence my previous question in Dumbing Down

Is it possible to teach mathematics to a larger range of students without compromising on the level taught?

PS I just have to add this quote from The Unapologetic Mathematician discussing this issue because it encapsulates what I have been trying to say for years though I fear it fell on deaf ears

The algorithm comes first, and understanding comes later. Mathematics simply is. It cannot be negotiated. Mathematics education as realized in the NCTM standards has been taken over by sociologists, or even Critical Theorists. They are vehemently opposed to the seemingly-authoritarian rote method and saying “just do it like this and don’t ask why”. Never mind the fact that in this case “why” comes naturally after “how”. And it’s about time for mathematicians to come down and start kicking some ass over this, or we’ll be left with nobody capable of replacing us.

Dumbing Down

There’s a fascinating post at The Unapologetic Mathematician called Math and science testing in public schools which says that, because many students are failing the current maths and science tests, Washington state is proposing that they should be replaced by easier end of course tests:

I went to public schools in Maryland, where we had similar exams. Those students sharing my cynical bent referred to them as the “functional idiot tests”. I really do mean that it mostly tested respiratory function. I passed two of them by filling in pseudorandom bubbles and never actually opening the test booklet.

This picture of dumbing down will be familiar to British readers. This quote from the same post

This is exactly what Washington state is about to do. The important thing is evidently not to teach mathematics or science to its students. It’s to draw the target after we know where they land — give them a test we know they can pass.

echoes some of the controversy over new GCSE Science exams to be taken by 16 year olds Critics attack new science GCSE. I have never met any mathematics teacher who isn’t convinced that mathematics in the UK has been dumbed down quite considerably. The one attempt in 2000 to redress this problem ended in miserable failure and so the slide downwards has continued.

But there’s another issue here. In Britain, over at least the last 100 years or more, there has been an attempt to democratise education in the sense that, where only elites stayed on at school beyond the age of 14 in the early 20th century, there are proposals to raise the school leaving age to 18 and ensure that 50% of the population go on to higher education. It means that studying mathematics is compulsory at least until the age of 16.

This is good but the effect has been to simplify the syllabus substantially to allow more students to succeed. Examination questions set in the early twentieth century on complicated algebraic manipulation or a question on inversion (see * below) set in 1962 could not be set now. So the question that needs to be asked is

Is it possible to teach mathematics to a larger range of students without compromising on the level taught?

Alexandre Borovik’s book Mathematics under the Microscope in the section 4.6 Mental arithmetic and the method of Radzivilovsky details a radical approach by “a brilliant and idiosyncratic mathematics teacher, Vladimir Radzivilovsky” who

systematically builds bridges between various mental presentations of order and number in his pupils’ heads

and

Radzivilovsky’s success is measured by the fact that, among his former students, he can name dozens of professional mathematicians, physicists and computer scientists

There must be others who have ideas about teaching mathematics to a wide range of students whilst still maintaining standards.

* Here is an inversion question taken from a University of London A level Paper III Summer 1962:

Prove that the inverse of the point with respect to the circle is

Find the equations of the inverses of the circles

and

with respect to the circle .

Deduce that and intersect at right angles.

A Levels

Last Thursday the A level results were announced and there were the usual recycled comments with some people attacking and others defending the system. There appears to be three main arguments used:

1. A levels are getting easier;
2. Teachers are getting better at preparing students for the exams;
3. Students work very hard and so it is insulting to them to say the exams are getting easier.

So let’s examine these arguments for A level maths, which is the subject I know about. Unlike some pundits I don’t wish to pontificate about subjects I am not familiar with. My main point is that the arguments above are not contradictory and it is quite possible for exams to be easier than in previous years and for students to find them hard.

1. It is generally acknowledged in the mathematical community that A level maths exams are getting easier and it has been remarked on by a government advisor  A-levels are easier says adviser. Yet this headline is misleading because it is only referring to maths and physics which shows just how difficult it is to have a rational argument about the standard of A levels.
   It is interesting to see the effect this is having on university mathematics courses even in the last few years A-Levels: Gah. 
   However, A level mathematics and its equivalent has become steadily easier over at least the last hundred years as the subject has been ‘democratised’ and taught to a wider population. I am very much in favour of this but the cost has been the dumbing down of the syllabus as I have mentioned before. I can only repeat my question that

   Is it possible to teach mathematics to a larger range of students without compromising on the level taught?

2. This is true but nothing to be proud about. Teachers and schools are under extraordinary pressure to get good results. Hence they teach very much to the exams, test and retest, and have no time to explore interesting parts of mathematics which would help to motivate and put things into context.
   How politicians can imply that this is good beats me.
3. Mathematics, as those of us who taught it know, is hard. This has been recognised (finally) by recent research, and it has been proposed that, as happens in Australia, more UCAS points are awarded for harder subjects like maths, though I can’t see that it will happen here.
   Also mathematics is essentially linear so unless students are adequately prepared at one stage they will find it very difficult to proceed to the next stage. With dumbing down going right back to the early years of education most students will find each stage hard no matter what the level. The ignorance of this caused disaster in 2000 when A level maths was temporarily made tougher and so the gap from GCSE was unbridgeable for many students, leading to lots of failures, the abandonment of the subject by many and the restoration of an easier system.
   Finally, with a greater percentage of the student population studying mathematics many of them are bound to find the subject hard.

It is good that Further Mathematics is becoming more popular and is to be encouraged, though it should be noticed that it too is a pale reflection of when it was last popular.

I don’t have easy answers to the problems of mathematical education but wish to see an informed debate on it. I just hope that Alexander Borovik is not correct when he writes

The current crisis in mathematics teaching is a dawn of a much more serious crisis of transition from the mass mathematics education of the past to a more selective and elitist education of increasingly small, in relative terms, numbers of mathematicians.

More on Maths Teaching in HE

Thanks to Gooseania for bringing to my attention a couple of interesting papers on teaching mathematics in US universities.

1. Teaching at the University Level by Steven Zucker explains how the student grading of course teaching can lead to dumbing down of courses. The teacher tends to please the student at the expense of covering the difficult parts of the mathematics course. The author believes that it would help greatly if students were to be told on arrival at university the huge difference in what is expected of them as compared to the schools they have just left.

It is unfortunate that in the UK it is so difficult to persuade non-mathematical teaching experts (so-called) that maths is hard and that I don’t expect students to understand it first-time round, which is why I spend so much time at the end of an A level course revising everything. It is true that at A level and beyond few students really understand the mathematics they have been taught until a year later (and after the exams) when they have to use it and suddenly the mist clears. I well remember looking back on a tough measure theory course that I didn’t really understand at the time, thinking ‘oh it’s obvious now’. It’s a natural part of learning mathematics and should be accepted as such.

2. Teaching Mathematics Graduate Students How to Teach by Solomon Friedberg is a paper on the usefulness of mathematical case studies for new university teachers who haven’t got the experience to judge how to pitch their courses. He gives a case study where a student argues that he should have got full marks in the following exam question (the italics are mine):

Let 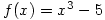. Use the definition of the derivative to compute the slope of the tangent line to the graph of 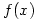at the point where .

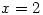The student questions why his answer only scores 5 marks out of 20. His answer was:

, . .

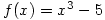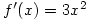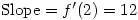The teacher fails to persuade the student of the importance of the method asked for.

Reading the question carefully and doing exactly what is asked for is a skill I have always taught A level and University students. Sometimes I even resort to “mathematics is not a democracy – you have to do as you are told” 🙂